Advertisements
Advertisements
प्रश्न
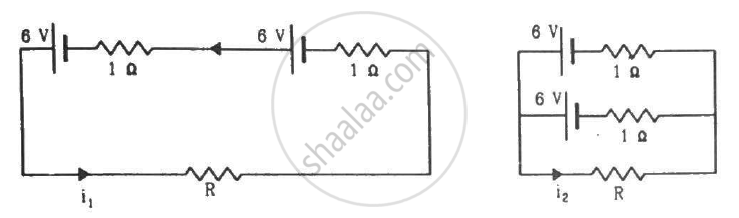
Find the value of i1/i2 in the following figure if (a) R = 0.1 Ω (b) R = 1 Ω and (c) R = 10 Ω. Note from your answers that in order to get more current from a combination of two batteries, they should be joined in parallel if the external resistance is small and in series if the external resistance is large, compared to the internal resistance.
उत्तर
(a) For R = 0.1 Ω
Applying KVL in the given circuit, we get:-
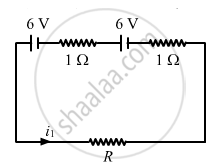
\[0 . 1 i_1 + 1 i_1 - 6 + 1 i_1 - 6 = 0\]
\[ \Rightarrow 0 . 1 i_1 + 1 i_1 + 1 i_1 = 12\]
\[ \Rightarrow i_1 = \frac{12}{\left( 2 . 1 \right)} = 5 . 71 A\]
Now, consider the given circuit.
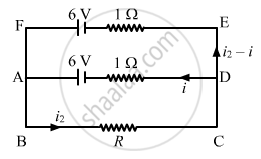
Applying KVL in the loop ABCDA, we get:-
\[0 . 1 i_2 + 1i - 6 = 0\]
\[ \Rightarrow 0 . 1 i_2 + i = 6\]
\[ \Rightarrow i = 6 - 0 . 1 i_2\]
Applying KVL in ADEFA, we get:-
\[i - 6 + 6 - \left( i_2 - i \right)1 = 0\]
\[ \Rightarrow i - i_2 + i = 0\]
\[ \Rightarrow 2i - i_2 = 0\]
\[ \Rightarrow 2\left[ 6 - 0 . 1 i_2 \right] - i_2 = 0\]
\[ \Rightarrow i_2 = 10 A\]
\[\therefore \frac{i_1}{i_2} = 0 . 571\]
(b) For R = 1 Ω
Applying KVL in the circuit given in figure 1, we get:-
\[1 i_1 + 1 . i_1 - 6 + i_1 - 6 = 0\]
\[ \Rightarrow 3 i_1 = 12\]
\[ \Rightarrow i_1 = 4\]
Now, for figure 2:-
Applying KVL in ABCDA, we get:-
\[i_2 + i - 6 = 0\]
\[ \Rightarrow i_2 + i = 6\]
Applying KVL in ADEFA, we get:-
\[i - 6 + 6 - \left( i_2 - i \right)1 = 0\]
\[ \Rightarrow i - i_2 + i = 0\]
\[ \Rightarrow 2i - i_2 = 0\]
\[ \Rightarrow 2\left[ 6 - i_2 \right] - i_2 = 0\]
\[ \Rightarrow 12 - 3 i_2 = 0\]
\[ \Rightarrow i_2 = 4 A\]
\[ \therefore \frac{i_1}{i_2} = 1\]
(c) For R = 10 Ω
Applying KVL in the circuit given in figure 1, we get:-
\[10 i_1 + 1 i_1 - 6 + 1 i_1 - 6 = 0\]
\[\Rightarrow 12 i_1 = 12\]
\[ \Rightarrow i_1 = 1\]
Now, for figure 2:-
Applying KVL in ABCDA, we get:-
\[10 i_2 + i - 6 = 0\]
\[ \Rightarrow i = 6 - 10 i_2\]
Applying KVL in ADEFA, we get:-
\[i - 6 + 6 - \left( i_2 - i \right)1 = 0\]
\[ \Rightarrow i - i_2 + i = 0\]
\[ \Rightarrow 2i - i_2 = 0\]
\[ \Rightarrow 2\left[ 6 - 10 i_2 \right] - i_2 = 0\]
\[ \Rightarrow 12 - 21 i_2 = 0\]
\[ \Rightarrow i_2 = 0 . 57 A\]
\[ \therefore \frac{i_1}{i_2} = 1 . 75\]
APPEARS IN
संबंधित प्रश्न
Two identical cells of emf 1.5 V each joined in parallel, supply energy to an external circuit consisting of two resistances of 7 Ω each joined in parallel. A very high resistance voltmeter reads the terminal voltage of cells to be 1.4 V. Calculate the internal resistance of each cell.
The storage battery of a car has an emf of 12 V. If the internal resistance of the battery is 0.4 Ω, what is the maximum current that can be drawn from the battery?
The earth’s surface has a negative surface charge density of 10−9 C m−2. The potential difference of 400 kV between the top of the atmosphere and the surface results (due to the low conductivity of the lower atmosphere) in a current of only 1800 A over the entire globe. If there were no mechanism of sustaining atmospheric electric field, how much time (roughly) would be required to neutralise the earth’s surface? (This never happens in practice because there is a mechanism to replenish electric charges, namely the continual thunderstorms and lightning in different parts of the globe). (Radius of earth = 6.37 × 106 m.)
A resistor R is connected to a cell of-emf e and internal resistance r. The potential difference across the resistor R is found to be V. State the relation between e, V, Rand r.
Two identical cells, each of emf E, having negligible internal resistance, are connected in parallel with each other across an external resistance R. What is the current through this resistance?
A rectangular conductor LMNO is placed in a uniform magnetic field of 0.5 T. The field is directed perpendicular to the plane of the conductor. When the arm MN of length of 20 cm is moved towards left with a velocity of 10 ms−1, calculate the emf induced in the arm. Given the resistance of the arm to be 5 Ω (assuming that other arms are of negligible resistance) find the value of the current in the arm.
A cell of emf E and internal resistance r is connected to two external resistance R1 and R2 and a perfect ammeter. The current in the circuit is measured in four different situations:
(i) without any external resistance in the circuit
(ii) with resistance R1 only
(iii) with R1 and R2 in series combination
(iv) with R1 and R2 in parallel combination
The currents measured in the four cases are 0.42 A, 1.05 A, 1.4 A and 4.2 A, but not necessarily in the order. Identify the currents corresponding to the four cases mentioned above.
Two cells of emf E1, E2 and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure.

Deduce the expressions for
(1) the equivalent e.m.f of the combination
(2) the equivalent resistance of the combination, and
(3) the potential difference between the point A and B.
Can the potential difference across a battery be greater than its emf?
Apply the first law of thermodynamics to a resistor carrying a current i. Identify which of the quantities ∆Q, ∆U and ∆W are zero, positive and negative.
Do all thermocouples have a neutral temperature?
Do the electrodes in an electrolytic cell have fixed polarity like a battery?
A coil of resistance 100 Ω is connected across a battery of emf 6.0 V. Assume that the heat developed in the coil is used to raise its temperature. If the heat capacity of the coil is 4.0 J K−1, how long will it take to raise the temperature of the coil by 15°C?
The temperatures of the junctions of a bismuth-silver thermocouple are maintained at 0°C and 0.001°C. Find the thermo-emf (Seebeck emf) developed. For bismuth-silver, a = − 46 × 10−6 V°C−1 and b = −0.48 × 10−6 V°C−2.
A plate of area 10 cm2 is to be electroplated with copper (density 9000 kg m−3) to a thickness of 10 micrometres on both sides, using a cell of 12 V. Calculate the energy spent by the cell in the process of deposition. If this energy is used to heat 100 g of water, calculate the rise in the temperature of the water. ECE of copper = 3 × 10−7 kg C−1and specific heat capacity of water = 4200 J kg−1.
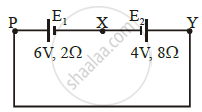
A cell E1 of emf 6 V and internal resistance 2 Ω is connected with another cell E2 of emf 4 V and internal resistance 8 Ω (as shown in the figure). The potential difference across points X and Y is ______.
A battery of EMF 10V sets up a current of 1A when connected across a resistor of 8Ω. If the resistor is shunted by another 8Ω resistor, what would be the current in the circuit? (in A)
Three cells, each of emf E but internal resistances 2r, 3r and 6r are connected in parallel across a resistor R.
Obtain expressions for (i) current flowing in the circuit, and (ii) the terminal potential differences across the equivalent cell.
An ac generator generates an emf which is given by e = 311 sin (240 πt) V. Calculate:
- frequency of the emf.
- r.m.s. value of the emf.
