Advertisements
Advertisements
प्रश्न
A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of grinding/cutting machine and sprayer. It takes 2 hours on the grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp while it takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at most 20 hours and the grinding/cutting machine for at most 12 hours. The profit from the sale of a lamp is ₹5.00 and a shade is ₹3.00. Assuming that the manufacturer sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit?
उत्तर
Suppose x units of pedestal lamps and y units of wooden shades are produced on a day to maximise the profit.
Since a pedestal lamp requires 2 hours on the grinding/cutting machine and a wooden shade requires 1 hour on the grinding/cutting machine, therefore, the total hours required for grinding/cutting x units of pedestal lamps and y units of wooden shades are (2x + y). But, the grinding/cutting machine is available for at most 12 hours on a day.
∴ 2x + y ≤ 12
Similarly, a pedestal lamp requires 3 hours on the sprayer and a wooden shade requires 2 hours on the sprayer, therefore, the total hours required for spraying x units of pedestal lamps and y units of wooden shades are (3x + 2y). But, the sprayer is available for at most 20 hours on a day.
∴ 3x + 2y ≤ 20
The profit from the sale of a pedestal lamp is ₹5.00 and a wooden shade is ₹3.00. Therefore, the total profit from the sale of x units of pedestal lamps and y units of wooden shades is ₹(5x + 3y).
Thus, the given linear programming problem is
Maximise Z = 5x + 3y
subject to the constraints
2x + y ≤ 12
3x + 2y ≤ 20
x, y ≥ 0
The feasible region determined by the given constraints can be diagrammatically represented as,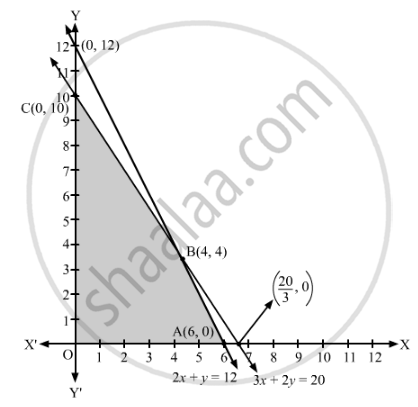
The coordinates of the corner points of the feasible region are O(0, 0), A(6, 0), B(4, 4) and C(0, 10).
The value of the objective function at these points are given in the following table.
| Corner Point | Z = 5x + 3y |
| (0, 0) | 5 × 0 + 3 × 0 = 0 |
| (6, 0) | 5 × 6 + 3 × 0 = 30 |
| (4, 4) | 5 × 4 + 3 × 4 = 32 → Maximum |
| (0, 10) | 5 × 0 + 3 × 10 = 30 |
The maximum value of Z is 32 at x = 4, y = 4.
Hence, the manufacturer should produce 4 pedestal lamps and 4 wooden shades to maximise his profit. The maximum profit of the manufacturer is ₹32 on a day.
APPEARS IN
संबंधित प्रश्न
Minimize `z=4x+5y ` subject to `2x+y>=7, 2x+3y<=15, x<=3,x>=0, y>=0` solve using graphical method.
Minimize : Z = 6x + 4y
Subject to the conditions:
3x + 2y ≥ 12,
x + y ≥ 5,
0 ≤ x ≤ 4,
0 ≤ y ≤ 4
Solve the following L.P.P graphically:
Maximize: Z = 10x + 25y
Subject to: x ≤ 3, y ≤ 3, x + y ≤ 5, x ≥ 0, y ≥ 0
Minimize :Z=6x+4y
Subject to : 3x+2y ≥12
x+y ≥5
0 ≤x ≤4
0 ≤ y ≤ 4
There are two types of fertilisers 'A' and 'B'. 'A' consists of 12% nitrogen and 5% phosphoric acid whereas 'B' consists of 4% nitrogen and 5% phosphoric acid. After testing the soil conditions, farmer finds that he needs at least 12 kg of nitrogen and 12 kg of phosphoric acid for his crops. If 'A' costs Rs 10 per kg and 'B' cost Rs 8 per kg, then graphically determine how much of each type of fertiliser should be used so that nutrient requirements are met at a minimum cost
A manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at Rs 7 profit and B at a profit of Rs 4. Find the production level per day for maximum profit graphically.
Solve the following L. P. P. graphically:Linear Programming
Minimize Z = 6x + 2y
Subject to
5x + 9y ≤ 90
x + y ≥ 4
y ≤ 8
x ≥ 0, y ≥ 0
In order to supplement daily diet, a person wishes to take X and Y tablets. The contents (in milligrams per tablet) of iron, calcium and vitamins in X and Y are given as below :
| Tablets | Iron | Calcium | Vitamin |
| x | 6 | 3 | 2 |
| y | 2 | 3 | 4 |
The person needs to supplement at least 18 milligrams of iron, 21 milligrams of calcium and 16 milligrams of vitamins. The price of each tablet of X and Y is Rs 2 and Rs 1 respectively. How many tablets of each type should the person take in order to satisfy the above requirement at the minimum cost? Make an LPP and solve graphically.
Maximize Z = 10x + 6y
Subject to
\[3x + y \leq 12\]
\[2x + 5y \leq 34\]
\[ x, y \geq 0\]
Minimize Z = 5x + 3y
Subject to
\[2x + y \geq 10\]
\[x + 3y \geq 15\]
\[ x \leq 10\]
\[ y \leq 8\]
\[ x, y \geq 0\]
Maximize Z = x + y
Subject to
\[- 2x + y \leq 1\]
\[ x \leq 2\]
\[ x + y \leq 3\]
\[ x, y \geq 0\]
Maximize Z = 3x + 3y, if possible,
Subject to the constraints
\[x - y \leq 1\]
\[x + y \geq 3\]
\[ x, y \geq 0\]
Solved the following linear programming problem graphically:
Maximize Z = 60x + 15y
Subject to constraints
\[x + y \leq 50\]
\[3x + y \leq 90\]
\[ x, y \geq 0\]
Find graphically, the maximum value of Z = 2x + 5y, subject to constraints given below:
2x + 4y ≤ 8
3x + y ≤ 6
x + y ≤ 4
x ≥ 0, y ≥ 0
Solve the following LPP graphically:
Maximize Z = 20 x + 10 y
Subject to the following constraints
\[x +\]2\[y \leq\]28
3x+ \[y \leq\]24
\[x \geq\] 2x.
\[y \geq\] 0
A wholesale dealer deals in two kinds, A and B (say) of mixture of nuts. Each kg of mixture A contains 60 grams of almonds, 30 grams of cashew nuts and 30 grams of hazel nuts. Each kg of mixture B contains 30 grams of almonds, 60 grams of cashew nuts and 180 grams of hazel nuts. The remainder of both mixtures is per nuts. The dealer is contemplating to use mixtures A and B to make a bag which will contain at least 240 grams of almonds, 300 grams of cashew nuts and 540 grams of hazel nuts. Mixture A costs Rs 8 per kg. and mixture B costs Rs 12 per kg. Assuming that mixtures A and B are uniform, use graphical method to determine the number of kg. of each mixture which he should use to minimise the cost of the bag.
One kind of cake requires 200 g of flour and 25 g of fat, and another kind of cake requires 100 g of flour and 50 g of fat. Find the maximum number of cakes which can be made from 5 kg of flour and 1 kg of fat assuming that there is no storage of the other ingredients used in making the cakes.
A farmer mixes two brands P and Q of cattle feed. Brand P, costing ₹250 per bag, contains 2 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing ₹200 per bag contains 1.5 units of nutritional element A, 11.25 units of element B and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
A manufacturer makes two types A and B of tea-cups. Three machines are needed for the manufacture and the time in minutes required for each cup on the machines is given below:
| Machines | |||
| I | II | III | |
| A B |
12 6 |
18 0 |
6 9 |
Each machine is available for a maximum of 6 hours per day. If the profit on each cup A is 75 paise and that on each cup B is 50 paise, show that 15 tea-cups of type A and 30 of type B should be manufactured in a day to get the maximum profit.
A factory owner purchases two types of machines, A and B, for his factory. The requirements and limitations for the machines are as follows:
| Area occupied by the machine |
Labour force for each machine |
Daily output in units |
|
| Machine A Machine B |
1000 sq. m 1200 sq. m |
12 men 8 men |
60 40 |
He has an area of 7600 sq. m available and 72 skilled men who can operate the machines.
How many machines of each type should he buy to maximize the daily output?
A firm manufacturing two types of electric items, A and B, can make a profit of Rs 20 per unit of A and Rs 30 per unit of B. Each unit of A requires 3 motors and 4 transformers and each unit of B requires 2 motors and 4 transformers. The total supply of these per month is restricted to 210 motors and 300 transformers. Type B is an export model requiring a voltage stabilizer which has a supply restricted to 65 units per month. Formulate the linear programing problem for maximum profit and solve it graphically.
A company manufactures two types of novelty Souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours available for assembling. The profit is 50 paise each for type A and 60 paise each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximize the profit?
There are two factories located one at place P and the other at place Q. From these locations, a certain commodity is to be delivered to each of the three depots situated at A, B and C. The weekly requirements of the depots are respectively 5, 5 and 4 units of the commodity while the production capacity of the factories at P and Q are respectively 8 and 6 units. The cost of transportation per unit is given below:
| From \ To | Cost (in ₹) | ||
| A | B | C | |
| P | 160 | 100 | 150 |
| Q | 100 | 120 | 100 |
How many units should be transported from each factory to each depot in order that the transportation cost is minimum. What will be the minimum transportation cost?
A manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at ₹7 profit and that of B at a profit of ₹4. Find the production level per day for maximum profit graphically.
A small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes one hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is Rs 100 and that on a bracelet is Rs 300. Formulate on L.P.P. for finding how many of each should be produced daily to maximize the profit?
It is being given that at least one of each must be produced.
Tow godowns, A and B, have grain storage capacity of 100 quintals and 50 quintals respectively. They supply to 3 ration shops, D, E and F, whose requirements are 60, 50 and 40 quintals respectively. The cost of transportation per quintal from the godowns to the shops are given in the following table:
| Transportation cost per quintal(in Rs.) | ||
| From-> | A | B |
| To | ||
| D | 6.00 | 4.00 |
| E | 3.00 | 2.00 |
| F | 2.50 | 3.00 |
How should the supplies be transported in order that the transportation cost is minimum?
By graphical method, the solution of linear programming problem
\[\text{ Subject } to \text{ 3 } x_1 + 2 x_2 \leq 18\]
\[ x_1 \leq 4\]
\[ x_2 \leq 6\]
\[ x_1 \geq 0, x_2 \geq 0, \text{ is } \]
The value of objective function is maximum under linear constraints ______.
A farmer has a supply of chemical fertilizer of type A which contains 10% nitrogen and 6% phosphoric acid and of type B which contains 5% nitrogen and 10% phosphoric acid. After the soil test, it is found that at least 7 kg of nitrogen and the same quantity of phosphoric acid is required for a good crop. The fertilizer of type A costs ₹ 5.00 per kg and the type B costs ₹ 8.00 per kg. Using Linear programming, find how many kilograms of each type of fertilizer should be bought to meet the requirement and for the cost to be minimum. Find the feasible region in the graph.
A company manufactures two types of products A and B. Each unit of A requires 3 grams of nickel and 1 gram of chromium, while each unit of B requires 1 gram of nickel and 2 grams of chromium. The firm can produce 9 grams of nickel and 8 grams of chromium. The profit is ₹ 40 on each unit of the product of type A and ₹ 50 on each unit of type B. How many units of each type should the company manufacture so as to earn a maximum profit? Use linear programming to find the solution.
The maximum value of z = 6x + 8y subject to x - y ≥ 0, x + 3y ≤ 12, x ≥ 0, y ≥ 0 is ______.
The region XOY - plane which is represented by the inequalities -5 ≤ x ≤ 5, -5 ≤ y ≤ 5 is ______
The point which provides the solution to the linear programming problem: Max P = 2x + 3y subject to constraints: x ≥ 0, y ≥ 0, 2x + 2y ≤ 9, 2x + y ≤ 7, x + 2y ≤ 8, is ______
Solve the following Linear Programming problem graphically:
Maximize: Z = 3x + 3.5y
Subject to constraints:
x + 2y ≥ 240,
3x + 1.5y ≥ 270,
1.5x + 2y ≤ 310,
x ≥ 0, y ≥ 0.
Solve the following Linear Programming Problem graphically:
Maximize: P = 70x + 40y
Subject to: 3x + 2y ≤ 9,
3x + y ≤ 9,
x ≥ 0,y ≥ 0.
Find feasible solution for the following system of linear inequation graphically.
3x + 4y ≥ 12, 4x + 7y ≤ 28, x ≥ 0, y ≥ 0
