Advertisements
Advertisements
प्रश्न
A cubic vessel (with faces horizontal + vertical) contains an ideal gas at NTP. The vessel is being carried by a rocket which is moving at a speed of 500 ms–1 in vertical direction. The pressure of the gas inside the vessel as observed by us on the ground ______.
पर्याय
remains the same because 500 ms−1 is very much smaller than vrms of the gas.
remains the same because motion of the vessel as a whole does not affect the relative motion of the gas molecules and the walls.
will increase by a factor equal to `(v_(rms)^2 + (500)^2)/v_(rms)^2` where vrms was the original mean square velocity of the gas.
will be different on the top wall and bottom wall of the vessel.
उत्तर
A cubic vessel (with faces horizontal + vertical) contains an ideal gas at NTP. The vessel is being carried by a rocket which is moving at a speed of 500 ms–1 in vertical direction. The pressure of the gas inside the vessel as observed by us on the ground remains the same because motion of the vessel as a whole does not affect the relative motion of the gas molecules and the walls.
Explanation:
According to the ideal gas law,
P = nRT/V, here temperature of the vessel remains unchanged hence, the pressure remains the same from that point of view.
Now, let us discuss the phenomenon inside the vessel. The gas molecules keep on colliding among themselves as well as with the walls of containing vessel. These collisions are perfectly elastic.
The number of collisions per unit volume in a gas remains constant. So, the pressure of the gas inside the vessel remains the same because the motion of the vessel as a whole does not affect the relative motion of the gas molecules with respect to the walls.
APPEARS IN
संबंधित प्रश्न
The energy of a given sample of an ideal gas depends only on its
The average momentum of a molecule in a sample of an ideal gas depends on
An ideal gas (Cp / Cv = γ) is taken through a process in which the pressure and the volume vary as p = aVb. Find the value of b for which the specific heat capacity in the process is zero.
Two ideal gases have the same value of Cp / Cv = γ. What will be the value of this ratio for a mixture of the two gases in the ratio 1 : 2?
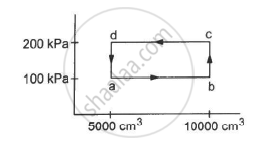
Half mole of an ideal gas (γ = 5/3) is taken through the cycle abcda, as shown in the figure. Take `"R" = 25/3"J""K"^-1 "mol"^-1 `. (a) Find the temperature of the gas in the states a, b, c and d. (b) Find the amount of heat supplied in the processes ab and bc. (c) Find the amount of heat liberated in the processes cd and da.
Consider a given sample of an ideal gas (Cp/Cv = γ) having initial pressure p0 and volume V0. (a) The gas is isothermally taken to a pressure p0/2 and from there, adiabatically to a pressure p0/4. Find the final volume. (b) The gas is brought back to its initial state. It is adiabatically taken to a pressure p0/2 and from there, isothermally to a pressure p0/4. Find the final volume.
Two vessels A and B of equal volume V0 are connected by a narrow tube that can be closed by a valve. The vessels are fitted with pistons that can be moved to change the volumes. Initially, the valve is open and the vessels contain an ideal gas (Cp/Cv = γ) at atmospheric pressure p0 and atmospheric temperature T0. The walls of vessel A are diathermic and those of B are adiabatic. The valve is now closed and the pistons are slowly pulled out to increase the volumes of the vessels to double the original value. (a) Find the temperatures and pressures in the two vessels. (b) The valve is now opened for sufficient time so that the gases acquire a common temperature and pressure. Find the new values of the temperature and pressure.
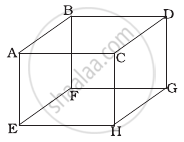
1 mole of an ideal gas is contained in a cubical volume V, ABCDEFGH at 300 K (Figure). One face of the cube (EFGH) is made up of a material which totally absorbs any gas molecule incident on it. At any given time ______.
When an ideal gas is compressed adiabatically, its temperature rises: the molecules on the average have more kinetic energy than before. The kinetic energy increases ______.
- because of collisions with moving parts of the wall only.
- because of collisions with the entire wall.
- because the molecules gets accelerated in their motion inside the volume.
- because of redistribution of energy amongst the molecules.
The container shown in figure has two chambers, separated by a partition, of volumes V1 = 2.0 litre and V2 = 3.0 litre. The chambers contain µ1 = 4.0 and µ2 = 5.0 moles of a gas at pressures p1 = 1.00 atm and p2 = 2.00 atm. Calculate the pressure after the partition is removed and the mixture attains equilibrium.
| V1 | V2 |
| µ1, p1 | µ2 |
| p2 |
