Advertisements
Advertisements
प्रश्न
When an ideal gas is compressed adiabatically, its temperature rises: the molecules on the average have more kinetic energy than before. The kinetic energy increases ______.
- because of collisions with moving parts of the wall only.
- because of collisions with the entire wall.
- because the molecules gets accelerated in their motion inside the volume.
- because of redistribution of energy amongst the molecules.
उत्तर
a
Explanation:
The mean free path becomes smaller because the ideal gas constricts, thus escalating the number of collisions per second among the molecules and walls. Because of which the temperature of gas increases which in turn escalates the Kinetic energy of gas molecules. Kinetic energy relies on temperature.
APPEARS IN
संबंधित प्रश्न
The energy of a given sample of an ideal gas depends only on its
Which of the following quantities is zero on an average for the molecules of an ideal gas in equilibrium?
Calculate the volume of 1 mole of an ideal gas at STP.
Find the number of molecules in 1 cm3 of an ideal gas at 0°C and at a pressure of 10−5mm of mercury.
Use R = 8.31 J K-1 mol-1
Let Q and W denote the amount of heat given to an ideal gas and the work done by it in an adiabatic process.
(a) Q = 0
(b) W = 0
(c) Q = W
(d) Q ≠ W
A rigid container of negligible heat capacity contains one mole of an ideal gas. The temperature of the gas increases by 1° C if 3.0 cal of heat is added to it. The gas may be
(a) helium
(b) argon
(c) oxygen
(d) carbon dioxide
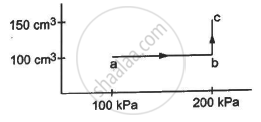
An ideal gas (γ = 1.67) is taken through the process abc shown in the figure. The temperature at point a is 300 K. Calculate (a) the temperatures at b and c (b) the work done in the process (c) the amount of heat supplied in the path ab and in the path bcand (d) the change in the internal energy of the gas in the process.
1 litre of an ideal gas (γ = 1.5) at 300 K is suddenly compressed to half its original volume. (a) Find the ratio of the final pressure to the initial pressure. (b) If the original pressure is 100 kPa, find the work done by the gas in the process. (c) What is the change in internal energy? (d) What is the final temperature? (e) The gas is now cooled to 300 K keeping its pressure constant. Calculate the work done during the process. (f) The gas is now expanded isothermally to achieve its original volume of 1 litre. Calculate the work done by the gas. (g) Calculate the total work done in the cycle.
The figure shows an adiabatic cylindrical tube of volume V0 divided in two parts by a frictionless adiabatic separator. Initially, the separator is kept in the middle, an ideal gas at pressure p1 and temperature T1 is injected into the left part and another ideal gas at pressure p2 and temperature T2 is injected into the right part. Cp/Cv = γ is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the volumes of the two parts (b) the heat given to the gas in the left part and (c) the final common pressure of the gases.

The container shown in figure has two chambers, separated by a partition, of volumes V1 = 2.0 litre and V2 = 3.0 litre. The chambers contain µ1 = 4.0 and µ2 = 5.0 moles of a gas at pressures p1 = 1.00 atm and p2 = 2.00 atm. Calculate the pressure after the partition is removed and the mixture attains equilibrium.
| V1 | V2 |
| µ1, p1 | µ2 |
| p2 |
