Advertisements
Advertisements
प्रश्न
Calculate the number of atoms in 39.4 g gold. Molar mass of gold is 197g mole–1.
उत्तर
We know that,
Molar mass = Mass of Avogadro's number of atoms (Molecules).
= 6.023 × 1023 atoms.
Given, molar mass of gold = 197 g/mol
Now,
∴ 197 g of gold contains = 6.023 × 1023 atoms
∴ 1 g of gold contain = `(6.023 xx 10^23)/197` atoms
∴ 39.4 g of gold contains = `(6.023 xx 10^23 xx 39.4)/197`
⇒ 1.20 × 1023 atoms.
APPEARS IN
संबंधित प्रश्न
Estimate the total number of air molecules (inclusive of oxygen, nitrogen, water vapour and other constituents) in a room of capacity 25.0 m3 at a temperature of 27 °C and 1 atm pressure
Match the following:
|
|
Column A |
Column B |
|
(a) |
cm3 |
(i) Pressure |
|
(b) |
Kelvin |
(ii) Temperature |
|
(c) |
Torr |
(iii) Volume |
|
(d) |
Boyle's law |
(iv) `"V"/"T" = ("V"_1)/("T"_1)` |
|
(a) |
Charles's law |
(v) `"PV"/"T" = ("P"_1 "V"_1)/"T"_1` |
|
|
|
(vi) PV = P1V1 |
Name or state the following:
The standard pressure of a gas in cm. of mercury corresponding to one atmospheric pressure.
Show that for diatomic gas the ratio of the two specific heats is 7:5.
Estimate the average thermal energy of a helium atom at the temperature on the surface of the Sun (6000 K).
Which of the following diagrams (Figure) depicts ideal gas behaviour?
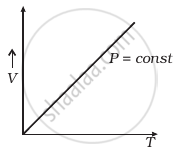 (a) |
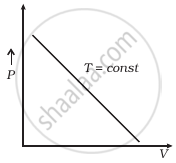 (b) |
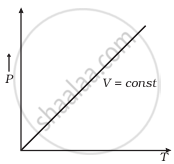 (c) |
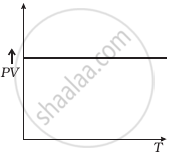 (d) |
A box of 1.00 m3 is filled with nitrogen at 1.50 atm at 300K. The box has a hole of an area 0.010 mm2. How much time is required for the pressure to reduce by 0.10 atm, if the pressure outside is 1 atm.
The volume V of an enclosure contains a mixture of three gases, 16 g of oxygen, 28 g of nitrogen and 44 g of carbon dioxide at absolute temperature T. Consider R as universal gas constant. The pressure of the mixture of gases is ______.
For a wave, y = 0.0002 sin`[2pi(110"t"-x/3)+pi/3]` is travelling in a medium. The energy per unit volume being transferred by wave if density of medium is 1.5 kg/m3, is ______.
Two tanks of equal volume contain equal mass of oxygen and nitrogen at 127°C. Find the ratio of pressure in two tanks.
