Advertisements
Advertisements
प्रश्न
A cyclist is travelling at 15 m s-1. She applies brakes so that she does not collide with a wall 18 m away. What deceleration must she have ?
उत्तर
We have to find the deceleration. We have the following information given,
Initial velocity, (u) = 15 m/s
Final velocity, (v) = 0 m/s
Distance travelled, (s) = 18 m
Let the acceleration be (a)
We can calculate acceleration by using the 3rd equation of motion,
`a = (v^2 - u^2)/(2s)`
Put the values in above equation to find the deceleration,
a = (0-225)/(36)
⇒ `a =-6.25 "m/s"^2`
Thus , the deceleration is 6.25 `"m/s"^2`
APPEARS IN
संबंधित प्रश्न
What is the nature of the distance-time graphs for uniform and non-uniform motion of an object?
Show the shape of the distance-time graph for the motion in the following case:
A car parked on a side road.
Figure shows the distance-time graph for the motion of two vehicles A and B. Which one of them is moving faster?
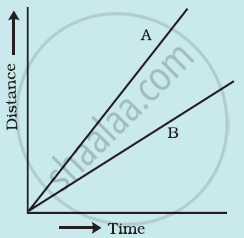
Figure: Distance-time graph for the motion of two cars
Which of the following distance-time graphs shows a truck moving with speed which is not constant?
Fill in the following blank with suitable word :
The slope of a speed-time graph of a moving body gives its………………………..
A car is travelling at 20 m/s along a road. A child runs out into the road 50 m ahead and the car driver steps on the brake pedal. What must the car’s deceleration be if the car is to stop just before it reaches the child ?
A spaceship is moving in space with a velocity of 60 kms−1. It fires its retro engines for 20 seconds and velocity is reduced to 55 kms−1. Calculate the distance travelled by a spaceship in 40 s, from the time of firing of the retro- rockets.
Two students were asked to plot a distance-time graph for the motion described in Table A and Table B.
Table A
| Distance moved (m) | 0 | 10 | 20 | 30 | 40 | 50 |
| Time (minutes) | 0 | 2 | 4 | 6 | 8 | 10 |
Table B
| Distance moved (m) | 0 | 5 | 10 | 15 | 20 | 25 |
| Time (minutes) | 0 | 1 | 2 | 3 | 4 | 5 |
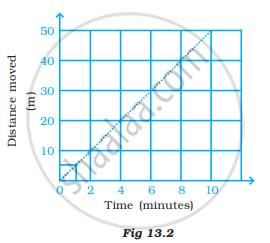
The graph given in Figure 13.2 is true for
If we denote speed by S, the distance by D and time by T, the relationship between these quantities is
Assertion: The slope of the distance-time graph of a body moving with high speed is steeper than the slope of the distance-time graph of a body with low velocity.
Reason: Slope of distance-time graph = speed of the body.
