Advertisements
Advertisements
Question
A cyclist is travelling at 15 m s-1. She applies brakes so that she does not collide with a wall 18 m away. What deceleration must she have ?
Solution
We have to find the deceleration. We have the following information given,
Initial velocity, (u) = 15 m/s
Final velocity, (v) = 0 m/s
Distance travelled, (s) = 18 m
Let the acceleration be (a)
We can calculate acceleration by using the 3rd equation of motion,
`a = (v^2 - u^2)/(2s)`
Put the values in above equation to find the deceleration,
a = (0-225)/(36)
⇒ `a =-6.25 "m/s"^2`
Thus , the deceleration is 6.25 `"m/s"^2`
APPEARS IN
RELATED QUESTIONS
What can you say about the motion of an object whose distance-time graph is a straight line parallel to the time axis?
Given figure shows the distance-time graph of three objects A, B and C. Study the graph and answer the following questions:
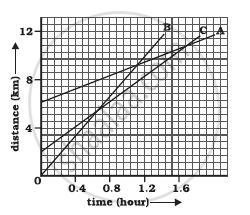
- Which of the three is travelling the fastest?
- Are all three ever at the same point on the road?
- How far has C travelled when B passes A?
- How far has B travelled by the time it passes C?
The speed-time graph for a car is shown in the following figure:
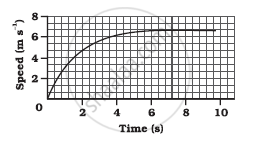
- Find how far the car travels in the first 4 seconds. Shade the area on the graph that represents the distance travelled by the car during the period.
- Which part of the graph represents uniform motion of the car?
Which of the following distance-time graphs shows a truck moving with speed which is not constant?
What can you say about the motion of a body whose distance-time graph is a straight line parallel to the time axis ?
A student draws a distance-time graph for a moving scooter and finds that a section of the graph is horizontal line parallel to the time axis. Which of the following conclusion is correct about this section of the graph?
Figure (a) shows the displacement-time graph for the motion of a body. Use it to calculate the velocity of the body at t = 1 s, 2 s and 3 s, and then draw the velocity-time graph in Figure (b) for it.
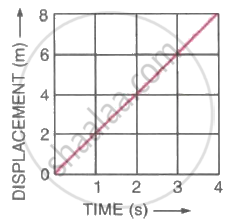 |
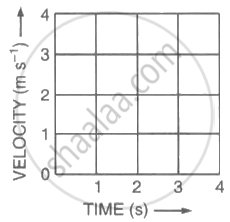 |
| (a) | (b) |
A body moves along a straight road with a speed of 20 m/s and has a uniform acceleration of 5 m/s2. What will be its speed after 2 s?
If we denote speed by S, the distance by D and time by T, the relationship between these quantities is
The slope of the distance-time graph indicates the speed.
