Advertisements
Advertisements
प्रश्न
A diverging lens of focal length 20 cm and a converging mirror of focal length 10 cm are placed coaxially at a separation of 5 cm. Where should an object be placed so that a real image is formed at the object itself?
उत्तर
Let the object be placed at a distance x cm from the lens (away from the mirror).
For the concave lens (Ist refraction) u = − x, f = − 20 cm
From lens formula:
\[\frac{1}{v} - \frac{1}{u} = \frac{1}{f}\Rightarrow\frac{1}{v}=\frac{1}{( - 20)}+\frac{1}{( - x)}\Rightarrow v=-\left( \frac{20x}{x + 20} \right)\]
Thus, the virtual image due to the first refraction lies on the same side as that of object (A'B').
This image becomes the object for the concave mirror,
For the mirror,
\[u = - \left( 5 + \frac{20x}{x + 20} \right)\]
\[ = - \left( \frac{25x + 100}{x + 20} \right)\]
\[f = - 10 \text{ cm }\]
From mirror equation,
\[\frac{1}{v} + \frac{1}{u} = \frac{1}{f}\]
\[ \Rightarrow \frac{1}{v} = \frac{1}{- 10} + \frac{x + 20}{25x + 100}\]
\[ \Rightarrow \frac{1}{v} = \frac{10x + 200 - 25x - 100}{250(x + 4)}\]
\[\Rightarrow v = \frac{250(x + 4)}{100 - 15x}\]
\[ \Rightarrow v = \frac{250(x + 4)}{15x - 100}\]
\[ \Rightarrow v = \frac{50(x + 4)}{(3x - 20)}\]
Thus, this image is formed towards left of the mirror.
Again for second refraction in concave lens,
\[u = - \left[ \frac{5 - 50(x + 4)}{3x - 20} \right]\]
(assuming that image of mirror is formed between the lens and mirror 3x − 20),
v = + x (since the final image is produced on the object A"B")
using lens formula,
\[\frac{1}{v} - \frac{1}{u} = \frac{1}{f}\]
\[ \Rightarrow \frac{1}{x}+\frac{1}{\frac{\left[ 5 - 50 (x \times 4) \right]}{3x - 20}}=\frac{1}{- 20}\]
⇒ 25x2 − 1400x − 6000 = 0
⇒ x2 − 56x − 240 = 0
⇒ (x − 60) (x + 4) = 0
So, x = 60 m
The object should be placed at a distance 60 cm from the lens farther away from the mirror, so that the final image is formed on itself.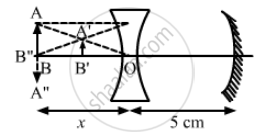
APPEARS IN
संबंधित प्रश्न
A double convex lens is made of a glass of refractive index 1.55, with both faces of the same radius of curvature. Find the radius of curvature required, if the focal length is 20 cm.
Can mirrors give rise to chromatic aberration?
In image formation from spherical mirrors, only paraxial rays are considered because they
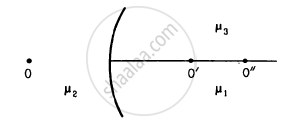
Following figure shows three transparent media of refractive indices \[\mu_1 , \mu_2 \text{ and } \mu_3\]. A point object O is placed in the medium \[\mu_2\]. If the entire medium on the right of the spherical surface has refractive index \[\mu_3\], the image forms at O". In the situation shown,
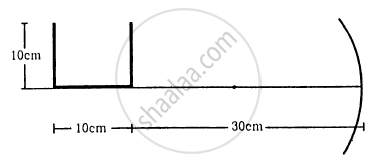
A U-shaped wire is placed before a concave mirror having radius of curvature 20 cm as shown in figure. Find the total length of the image.
A spherical surface of radius 30 cm separates two transparent media A and B with refractive indices 1.33 and 1.48 respectively. The medium A is on the convex side of the surface. Where should a point object be placed in medium A so that the paraxial rays become parallel after refraction at the surface?
A converging lens of focal length 12 cm and a diverging mirror of focal length 7.5 cm are placed 5.0 cm apart with their principal axes coinciding. Where should an object be placed so that its image falls on itself?
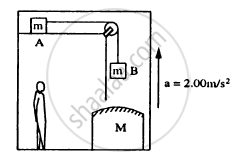
Consider the situation shown in figure. The elevator is going up with an acceleration of 2.00 m s−2 and the focal length of the mirror is 12.0 cm. All the surfaces are smooth and the pulley is light. The mass-pulley system is released from rest (with respect to the elevator) at t = 0 when the distance of B from the mirror is 42.0 cm. Find the distance between the image of the block B and the mirror at t = 0.200 s. Take g = 10 m s−2.
Two thin lenses having optical powers of -10D and+ 6D are placed in contact with each other. The focal length of the combination is:
Answer the following question.
Three lenses of focal length +10 cm, —10 cm and +30 cm are arranged coaxially as in the figure given below. Find the position of the final image formed by the combination.

Answer the following question.
With the help of a ray diagram, obtain the relation between its focal length and radius of curvature.
Focal length of a mirror is given by ______.
A thin converging lens of focal length 12 cm is kept in contact with a thin diverging lens of focal length 18 cm. Calculate the effective/equivalent focal length of the combination.
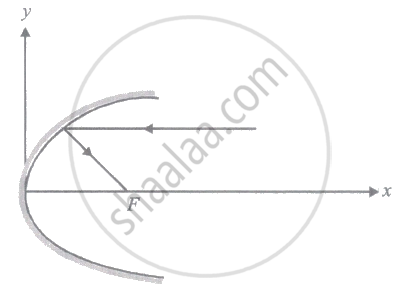
A parallel beam of light ray parallel to the x-axis is incident on a parabolic reflecting surface x = 2by2 as shown in the figure. After reflecting it passes through focal point F. What is the focal length of the reflecting surface?
An astronomical refractive telescope has an objective of focal length 20 m and an eyepiece of focal length 2 cm.
- The length of the telescope tube is 20.02 m.
- The magnification is 1000.
- The image formed is inverted.
- An objective of a larger aperture will increase the brightness and reduce chromatic aberration of the image.
A thin convex lens of focal length 25 cm is cut into two pieces 0.5 cm above the principal axis. The top part is placed at (0, 0) and an object placed at (– 50 cm, 0). Find the coordinates of the image.
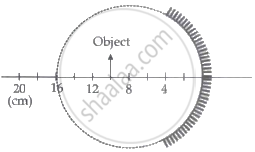
A spherical mirror is obtained as shown in the figure from a hollow glass sphere. if an object is positioned in front of the mirror, what will be the nature and magnification of the image of the object? (Figure drawn as schematic and not to scale)
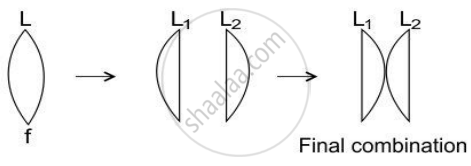
A lens of focal length f is divided into two equal parts and then these parts are put in a combination as shown in the figure below.
- What is the focal length of L1?
- What is the focal length of the final combination?