Advertisements
Advertisements
प्रश्न
A gas cylinder has walls that can bear a maximum pressure of 1.0 × 106 Pa. It contains a gas at 8.0 × 105 Pa and 300 K. The cylinder is steadily heated. Neglecting any change in the volume, calculate the temperature at which the cylinder will break.
उत्तर
Given:-
Maximum pressure that the cylinder can bear, Pmax = 1.0 × 106 Pa
Pressure in the gas cylinder, P1 = 8.0 × 105 Pa
Temperature in the cylinder, T1 = 300 K
Let T2 be the temperature at which the cylinder will break.
Volume is constant. Thus, ............(Given)
V1= V2 = V
Applying the five variable gas equation, we get
\[\frac{P_1 V}{T_1} = \frac{P_2 V}{T_2} .........( \because V_1 = V_2 )\]
\[ \Rightarrow \frac{P_1}{T_1} = \frac{P_2}{T_2}\]
\[ \Rightarrow T_2 = \frac{P_2 \times T_1}{P_1}\]
\[ \Rightarrow T_2 = \frac{1 . 0 \times {10}^6 \times 300}{8 . 0 \times {10}^5}=375K\]
APPEARS IN
संबंधित प्रश्न
When we place a gas cylinder on a van and the van moves, does the kinetic energy of the molecules increase? Does the temperature increase?
The pressure of an ideal gas is written as \[P = \frac{2E}{3V}\] . Here E refers to
An ideal gas is kept in a long cylindrical vessel fitted with a frictionless piston of cross-sectional area 10 cm2 and weight 1 kg in figure. The vessel itself is kept in a big chamber containing air at atmospheric pressure 100 kPa. The length of the gas column is 20 cm. If the chamber is now completely evacuated by an exhaust pump, what will be the length of the gas column? Assume the temperature to remain constant throughout the process.
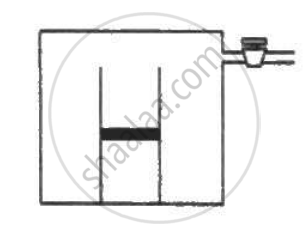
Figure shows two rigid vessels A and B, each of volume 200 cm3, containing an ideal gas (Cv = 12.5 J K−1 mol−1). The vessels are connected to a manometer tube containing mercury. The pressure in both the vessels is 75 cm of mercury and the temperature is 300 K. (a) Find the number of moles of the gas in each vessel. (b) 5.0 J of heat is supplied to the gas in vessel A and 10 J to the gas in vessel B. Assuming there's no appreciable transfer of heat from A to B, calculate the difference in the heights of mercury in the two sides of the manometer. Gas constant, R = 8.3 J K−1 mol−1.
Using figure, find the boiling point of methyl alcohol at 1 atm (760 mm of mercury) and at 0.5 atm.

If the density of oxygen is 1.44 kg/m3 at a pressure of 105 N/m2, find the root mean square velocity of oxygen molecules.
Energy is emitted from a hole in an electric furnace at the rate of 20 W when the temperature of the furnace is 727°C. What is the area of the hole? (Take Stefan’s constant σ to be 5.7 × 10-8 Js-1 m-2K-4.)
Under which condition laws of Boyle, Charles, and Gay-Lussac are valid?
Above what temperature, all bodies radiate electromagnetic radiation?
A metal cube of length 4 cm radiates heat at the rate of 10 J/s. Find its emissive power at a given temperature.
What is the microscopic origin of temperature?
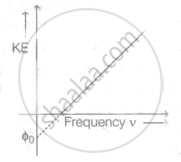
The graph of kinetic energy against the frequency v of incident light is as shown in the figure. The slope of the graph and intercept on X-axis respectively are ______.
The molecules of a given mass of a gas have root mean square speeds of 100 ms−1 at 27°C and 1.00 atmospheric pressure. What will be the root mean square speeds of the molecules of the gas at 127°C and 2.0 atmospheric pressure?
An insulated container containing monoatomic gas of molar mass m is moving with a velocity vo. If the container is suddenly stopped, find the change in temperature.
Consider a rectangular block of wood moving with a velocity v0 in a gas at temperature T and mass density ρ. Assume the velocity is along x-axis and the area of cross-section of the block perpendicular to v0 is A. Show that the drag force on the block is `4ρAv_0 sqrt((KT)/m)`, where m is the mass of the gas molecule.
When a particle oscillates simple harmonically, its kinetic energy varies periodically. If frequency of the particle is n, then the frequency of the kinetic energy is ______.
At what temperature will therms velocity of a gas be four times its value at STP?
If a = 0. 72 and r = 0.24, then the value of t is ______.
