Advertisements
Advertisements
प्रश्न
A largest sphere is to be carved out of a right circular cylinder of radius 7 cm and height 14 cm. Find the volume of the sphere.
उत्तर
Radius of largest sphere that can be formed inside the cylinder should be equal to the radius of the cylinder.
Radius of the largest sphere = 7 cm
Volume of sphere
= `4/3 pir^3`
= `4/3 xx 22/7 xx7 xx 7 xx 7`
= `4312/3`
= 1437 cm3
APPEARS IN
संबंधित प्रश्न
Find the surface area of a sphere of diameter 3.5 m.
`["Assume "pi=22/7]`
A right circular cylinder just encloses a sphere of radius r (see figure). Find
- surface area of the sphere,
- curved surface area of the cylinder,
- ratio of the areas obtained in (i) and (ii).

A model of a ship is made to a scale 1: 300
1) The length of the model of the ship is 2 m. Calculate the lengths of the ship.
2) The area of the deck ship is 180,000 m2. Calculate the area of the deck of the model.
3) The volume of the model in 6.5 m3. Calculate the volume of the ship.
On a map drawn to a scale of 1: 50,000, a rectangular plot of land ABCD has the following dimensions. AB = 6 cm; BC = 8 cm and all angles are right angles. Find:
1) the actual length of the diagonal distance AC of the plot in km.
2) the actual area of the plot in sq. km.
The surface area of a solid metallic sphere is 2464 cm2. It is melted and recast into solid right circular cones of radius 3.5 cm and height 7 cm. Calculate:
- the radius of the sphere.
- the number of cones recast. (Take π = `22/7`)
A solid sphere of radius 15 cm is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate the number of cones recast.
A hollow sphere of internal and external radii 6 cm and 8 cm respectively is melted and recast into small cones of base radius 2 cm and height 8 cm. Find the number of cones.
Find the total surface area of a hemisphere and a solid hemisphere each of radius 10 cm.
(Use 𝜋 = 3.14)
The dome of a building is in the form of a hemisphere. Its radius is 63 dm. Find the cost of
painting it at the rate of Rs. 2 per sq. m.
A cylinder of same height and radius is placed on the top of a hemisphere. Find the curved
surface area of the shape if the length of the shape be 7 cm.
A solid sphere of radius 15 cm is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate the number of cones recast.
A solid rectangular block of metal 49 cm by 44 cm by 18 cm is melted and formed into a solid sphere. Calculate the radius of the sphere.
What is the least number of solid metallic spheres, each of 6 cm diameter, that should be melted and recast to form a solid metal cone whose height is 45 cm and diameter 12 cm?
If a sphere is inscribed in a cube, find the ratio of the volume of cube to the volume of the sphere.
The largest sphere is cut off from a cube of side 6 cm. The volume of the sphere will be
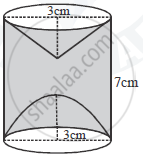
A hemispherical and a conical hole is scooped out of a.solid wooden cylinder. Find the volume of the remaining solid where the measurements are as follows:
The height of the solid cylinder is 7 cm, radius of each of hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm.
Give your answer correct to the nearest whole number.Taken`pi = 22/7`.
Find the volume and surface area of a sphere of diameter 21 cm.
A vessel is in he form of an inverted cone. Its height is 11 cm., and the radius of its top which is open is 2.5 cm. It is filled with water up to the rim. When lead shots, each of which is a sphere of radius 0.25 cm., are dropped 2 into the vessel, `2/5`th of the water flows out. Find the number of lead shots dropped into the vessel.
The radius of a sphere is 10 cm. If we increase the radius 5% then how many % will increase in volume?
The surface area of a solid metallic sphere is 616 cm2. It is melted and recast into smaller spheres of diameter 3.5 cm. How many such spheres can be obtained?
