Advertisements
Advertisements
प्रश्न
A particle moves along the X-axis as x = u (t − 2 s) + a (t − 2 s)2.
(a) the initial velocity of the particle is u
(b) the acceleration of the particle is a
(c) the acceleration of the particle is 2a
(d) at t = 2 s particle is at the origin.
उत्तर
(c) the acceleration of the particle is 2a
(d) at t = 2 s, the particle is at the origin
Initial velocity = \[\left| \frac{d x}{d t} \right|_{t = 0}\]
x = u(2 s − 2 s) + a (2 s − 2 s)2 = 0 (origin)
APPEARS IN
संबंधित प्रश्न
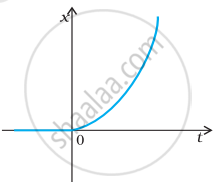
The figure shows the x-t plot of one-dimensional motion of a particle. Is it correct to say from the graph that the particle moves in a straight line for t < 0 and on a parabolic path for t > 0? If not, suggest a suitable physical context for this graph.
A police van moving on a highway with a speed of 30 km h–1 fires a bullet at a thief’s car speeding away in the same direction with a speed of 192 km h–1. If the muzzle speed of the bullet is 150 m s–1, with what speed does the bullet hit the thief’s car? (Note: Obtain that speed which is relevant for damaging the thief’s car).
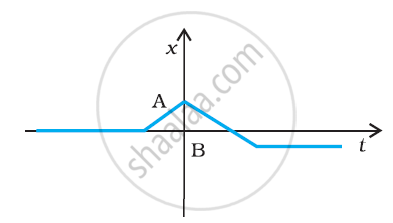
Suggest a suitable physical situation for the following graphs:
Two projectiles A and B are projected with angle of projection 15° for the projectile A and 45° for the projectile B. If RA and RB be the horizontal range for the two projectiles, then
A man has to go 50 m due north, 40 m due east and 20 m due south to reach a field. (a) What distance he has to walk to reach the field? (b) What is his displacement from his house to the field?
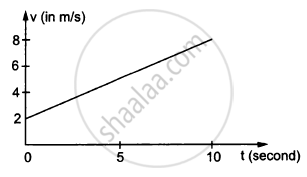
In the following figure Shows the graph of velocity versus time for a particle going along the X-axis. Find the acceleration
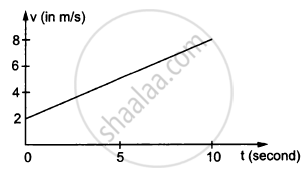
In the following figure Shows the graph of velocity versus time for a particle going along the X-axis. Find the distance travelled in 0 to 10s
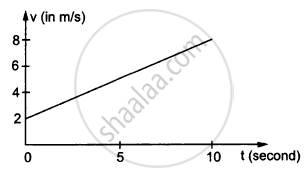
In the following figure Shows the graph of velocity versus time for a particle going along the X-axis. Find the displacement in 0 to 10 s.
Refer to the graphs in figure. Match the following.
| Graph | Characteristic |
(a) 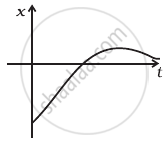 |
(i) has v > 0 and a < 0 throughout. |
(b) 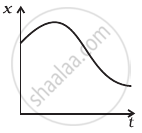 |
(ii) has x > 0 throughout and has a point with v = 0 and a point with a = 0. |
(c) 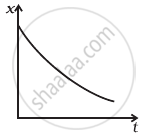 |
(iii) has a point with zero displacement for t > 0. |
(d)  |
(iv) has v < 0 and a > 0. |
A ball is dropped and its displacement vs time graph is as shown figure (displacement x is from ground and all quantities are +ve upwards).

- Plot qualitatively velocity vs time graph.
- Plot qualitatively acceleration vs time graph.
A man runs across the roof-top of a tall building and jumps horizontally with the hope of landing on the roof of the next building which is of a lower height than the first. If his speed is 9 m/s, the (horizontal) distance between the two buildings is 10 m and the height difference is 9 m, will he be able to land on the next building? (take g = 10 m/s2)
The velocity-displacement graph of a particle is shown in figure.
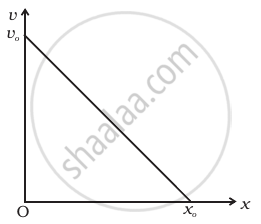
- Write the relation between v and x.
- Obtain the relation between acceleration and displacement and plot it.
Ship A is sailing towards the northeast with velocity `vecv = 30hati + 50hatj` km/hr where `hati` points east and `hatj`, north. Ship B is at a distance of 80 km east and 150 km north of Ship A and is sailing west at 10 km/hr. A will be at the minimum distance from B in ______.
A car covers the first half of the distance between two places at 40 km/h and other half at 60 km/h. The average speed of the car is ______.
