Advertisements
Advertisements
प्रश्न
A police jeep, approaching an orthogonal intersection from the northern direction, is chasing a speeding car that has turned and moving straight east. When the jeep is 0.6 km north of the intersection and the car is 0.8 km to the east. The police determine with a radar that the distance between them and the car is increasing at 20 km/hr. If the jeep is moving at 60 km/hr at the instant of measurement, what is the speed of the car?
उत्तर
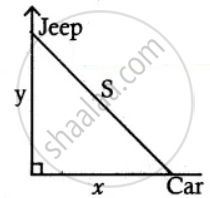
Given x = 0.8
y = 0.6
`("d"y)/"dt"` = – 60
`"ds"/"dtt"` = 20
From the figure
S2 = x2 + y2
S2 = (0.8)2 + (0.6)2
= 0.64 + 0.36
= 1
S2 = 1
⇒ S = 1
S2 = x2 + y2
Differentiating w.r.t. ‘t’
`2"S" "dS"/"dt" = 2x ("d"x)/"dt" + 2y ("d"y)/"dt"` .....(÷ 2)
`"S" "dS"/"dt" = x ("d"x)/"dt" + y ("d"y)/"dt"`
1(20) = `(0.8) ("d"x)/"dt" + (0.6)(- 60)`
20 = `0.8 ("d"x)/"dt" 36`
∴ `("d"x)/"dt" = (20 + 36)/0.8`
= `56/0.8`
= 70
∴ Speed of the car is 70 km/hr.
APPEARS IN
संबंधित प्रश्न
A particle moves along a straight line in such a way that after t seconds its distance from the origin is s = 2t2 + 3t metres. Find the average velocity between t = 3 and t = 6 seconds
A particle moves along a straight line in such a way that after t seconds its distance from the origin is s = 2t2 + 3t metres. Find the instantaneous velocities at t = 3 and t = 6 seconds
A camera is accidentally knocked off an edge of a cliff 400 ft high. The camera falls a distance of s = 16t2 in t seconds. How long does the camera fall before it hits the ground?
A camera is accidentally knocked off an edge of a cliff 400 ft high. The camera falls a distance of s = 16t2 in t seconds. What is the instantaneous velocity of the camera when it hits the ground?
A particle moves along a line according to the law s(t) = 2t3 – 9t2 + 12t – 4, where t ≥ 0. At what times the particle changes direction?
A particle moves along a line according to the law s(t) = 2t3 – 9t2 + 12t – 4, where t ≥ 0. Find the particle’s acceleration each time the velocity is zero
If the volume of a cube of side length x is v = x3. Find the rate of change of the volume with respect to x when x = 5 units
If the mass m(x) (in kilograms) of a thin rod of length x (in metres) is given by, m(x) = `sqrt(3x)` then what is the rate of change of mass with respect to the length when it is x = 3 and x = 27 metres
Find the slope of the tangent to the following curves at the respective given points.
y = x4 + 2x2 – x at x = 1
Find the slope of the tangent to the following curves at the respective given points.
x = a cos3t, y = b sin3t at t = `pi/2`
Find the tangent and normal to the following curves at the given points on the curve
y = x2 – x4 at (1, 0)
Find the tangent and normal to the following curves at the given points on the curve
x = cos t, y = 2 sin2t at t = `pi/2`
Show that the two curves x2 – y2 = r2 and xy = c2 where c, r are constants, cut orthogonally
Choose the correct alternative:
A balloon rises straight up at 10 m/s. An observer is 40 m away from the spot where the balloon left the ground. The rate of change of the balloon’s angle of elevation in radian per second when the balloon is 30 metres above the ground
Choose the correct alternative:
The slope of the line normal to the curve f(x) = 2 cos 4x at x = `pi/12` is
Choose the correct alternative:
The maximum slope of the tangent to the curve y = ex sin x, x ∈ [0, 2π] is at
