Advertisements
Advertisements
प्रश्न
A ray of light passing through the point (1, 2) reflects on the x-axis at point A and the reflected ray passes through the point (5, 3). Find the coordinates of A.
उत्तर
Let BC be the coordinate of that point A (a, 0) along the x-axis. AN is perpendicular to it. PA is an incident ray and AQ is a reflected ray.
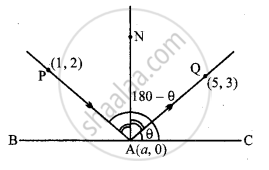
⇒ Angle of incidence PAN = Angle of reflection NAQ
⇒ ∠PAB = ∠QAC
⇒ If the inclination of QA is 0 then the inclination of PA will be 180 – θ.
Slope of QA when Q(5, 3) and A(a, 0) then
`tan θ = (0 - 3)/("a" - 5) = (-3)/("a" - 5)`
Slope of PA when P(1, 2) and A(a, 0), then
tan (180° - θ) = `(0 - 2)/("a" - 1)`
tan (180° - θ) = − tan θ
∴ `(-2)/("a" - 1) = (-3)/("a" - 5) = 3/("a" - 5)`
or −2(a − 5) = 3(a − 1)
or −2a + 10 = 3a − 3
or 5a = 13
or a = `13/5`
∴ The coordinates of point A is `(13/5, 0)`.
APPEARS IN
संबंधित प्रश्न
Find the distance of the point (–1, 1) from the line 12(x + 6) = 5(y – 2).
Find the points on the x-axis, whose distances from the `x/3 +y/4 = 1` are 4 units.
Find the distance between parallel lines:
15x + 8y – 34 = 0 and 15x + 8y + 31 = 0
Find the distance between parallel lines l (x + y) + p = 0 and l (x + y) – r = 0
Find the direction in which a straight line must be drawn through the point (–1, 2) so that its point of intersection with the line x + y = 4 may be at a distance of 3 units from this point.
Find the co-ordinates of the point, which divides the line segment joining the points A(2, − 6, 8) and B(− 1, 3, − 4) externally in the ratio 1 : 3.
A line a drawn through A (4, −1) parallel to the line 3x − 4y + 1 = 0. Find the coordinates of the two points on this line which are at a distance of 5 units from A.
The perpendicular distance of a line from the origin is 5 units and its slope is − 1. Find the equation of the line.
What are the points on X-axis whose perpendicular distance from the straight line \[\frac{x}{a} + \frac{y}{b} = 1\] is a ?
Show that the product of perpendiculars on the line \[\frac{x}{a} \cos \theta + \frac{y}{b} \sin \theta = 1\] from the points \[( \pm \sqrt{a^2 - b^2}, 0) \text { is }b^2 .\]
Find the perpendicular distance from the origin of the perpendicular from the point (1, 2) upon the straight line \[x - \sqrt{3}y + 4 = 0 .\]
What are the points on y-axis whose distance from the line \[\frac{x}{3} + \frac{y}{4} = 1\] is 4 units?
If the length of the perpendicular from the point (1, 1) to the line ax − by + c = 0 be unity, show that \[\frac{1}{c} + \frac{1}{a} - \frac{1}{b} = \frac{c}{2ab}\] .
Determine the distance between the pair of parallel lines:
8x + 15y − 34 = 0 and 8x + 15y + 31 = 0
Determine the distance between the pair of parallel lines:
y = mx + c and y = mx + d
Prove that the lines 2x + 3y = 19 and 2x + 3y + 7 = 0 are equidistant from the line 2x + 3y= 6.
Find the ratio in which the line 3x + 4y + 2 = 0 divides the distance between the line 3x + 4y + 5 = 0 and 3x + 4y − 5 = 0
Find the equations of the lines through the point of intersection of the lines x − y + 1 = 0 and 2x − 3y+ 5 = 0, whose distance from the point(3, 2) is 7/5.
If the centroid of a triangle formed by the points (0, 0), (cos θ, sin θ) and (sin θ, − cos θ) lies on the line y = 2x, then write the value of tan θ.
If the lines x + ay + a = 0, bx + y + b = 0 and cx + cy + 1 = 0 are concurrent, then write the value of 2abc − ab − bc − ca.
The line segment joining the points (−3, −4) and (1, −2) is divided by y-axis in the ratio
The area of a triangle with vertices at (−4, −1), (1, 2) and (4, −3) is
The line segment joining the points (1, 2) and (−2, 1) is divided by the line 3x + 4y = 7 in the ratio ______.
The ratio in which the line 3x + 4y + 2 = 0 divides the distance between the line 3x + 4y + 5 = 0 and 3x + 4y − 5 = 0 is
The shortest distance between the lines
`bar"r" = (hat"i" + 2hat"j" + hat"k") + lambda (hat"i" - hat"j" + hat"k")` and
`bar"r" = (2hat"i" - hat"j" - hat"k") + mu(2hat"i" + hat"j" + 2hat"k")` is
If P(α, β) be a point on the line 3x + y = 0 such that the point P and the point Q(1, 1) lie on either side of the line 3x = 4y + 8, then _______.
The distance of the point P(1, – 3) from the line 2y – 3x = 4 is ______.
The value of the λ, if the lines (2x + 3y + 4) + λ (6x – y + 12) = 0 are
| Column C1 | Column C2 |
| (a) Parallel to y-axis is | (i) λ = `-3/4` |
| (b) Perpendicular to 7x + y – 4 = 0 is | (ii) λ = `-1/3` |
| (c) Passes through (1, 2) is | (iii) λ = `-17/41` |
| (d) Parallel to x axis is | λ = 3 |
The distance of the point (2, – 3, 1) from the line `(x + 1)/2 = (y - 3)/3 = (z + 1)/-1` is ______.
