Advertisements
Advertisements
Question
A ray of light passing through the point (1, 2) reflects on the x-axis at point A and the reflected ray passes through the point (5, 3). Find the coordinates of A.
Advertisements
Solution
Let BC be the coordinate of that point A (a, 0) along the x-axis. AN is perpendicular to it. PA is an incident ray and AQ is a reflected ray.
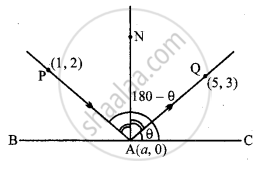
⇒ Angle of incidence PAN = Angle of reflection NAQ
⇒ ∠PAB = ∠QAC
⇒ If the inclination of QA is 0 then the inclination of PA will be 180 – θ.
Slope of QA when Q(5, 3) and A(a, 0) then
`tan θ = (0 - 3)/("a" - 5) = (-3)/("a" - 5)`
Slope of PA when P(1, 2) and A(a, 0), then
tan (180° - θ) = `(0 - 2)/("a" - 1)`
tan (180° - θ) = − tan θ
∴ `(-2)/("a" - 1) = (-3)/("a" - 5) = 3/("a" - 5)`
or −2(a − 5) = 3(a − 1)
or −2a + 10 = 3a − 3
or 5a = 13
or a = `13/5`
∴ The coordinates of point A is `(13/5, 0)`.
APPEARS IN
RELATED QUESTIONS
Find the equation of the line parallel to y-axis and drawn through the point of intersection of the lines x– 7y + 5 = 0 and 3x + y = 0.
Find the direction in which a straight line must be drawn through the point (–1, 2) so that its point of intersection with the line x + y = 4 may be at a distance of 3 units from this point.
Prove that the line y − x + 2 = 0 divides the join of points (3, −1) and (8, 9) in the ratio 2 : 3.
Find the equation of the line whose perpendicular distance from the origin is 4 units and the angle which the normal makes with the positive direction of x-axis is 15°.
Find the distance of the point (2, 5) from the line 3x + y + 4 = 0 measured parallel to the line 3x − 4y+ 8 = 0.
Find the distance of the point (4, 5) from the straight line 3x − 5y + 7 = 0.
Show that the perpendiculars let fall from any point on the straight line 2x + 11y − 5 = 0 upon the two straight lines 24x + 7y = 20 and 4x − 3y − 2 = 0 are equal to each other.
Show that the path of a moving point such that its distances from two lines 3x − 2y = 5 and 3x + 2y = 5 are equal is a straight line.
If sum of perpendicular distances of a variable point P (x, y) from the lines x + y − 5 = 0 and 3x − 2y + 7 = 0 is always 10. Show that P must move on a line.
Determine the distance between the pair of parallel lines:
8x + 15y − 34 = 0 and 8x + 15y + 31 = 0
Determine the distance between the pair of parallel lines:
y = mx + c and y = mx + d
Determine the distance between the pair of parallel lines:
4x + 3y − 11 = 0 and 8x + 6y = 15
The equations of two sides of a square are 5x − 12y − 65 = 0 and 5x − 12y + 26 = 0. Find the area of the square.
Prove that the lines 2x + 3y = 19 and 2x + 3y + 7 = 0 are equidistant from the line 2x + 3y= 6.
Find the ratio in which the line 3x + 4y + 2 = 0 divides the distance between the line 3x + 4y + 5 = 0 and 3x + 4y − 5 = 0
Find the equations of the lines through the point of intersection of the lines x − y + 1 = 0 and 2x − 3y+ 5 = 0, whose distance from the point(3, 2) is 7/5.
Write the value of θ ϵ \[\left( 0, \frac{\pi}{2} \right)\] for which area of the triangle formed by points O (0, 0), A (a cos θ, b sin θ) and B (a cos θ, − b sin θ) is maximum.
Write the distance between the lines 4x + 3y − 11 = 0 and 8x + 6y − 15 = 0.
If the lines x + ay + a = 0, bx + y + b = 0 and cx + cy + 1 = 0 are concurrent, then write the value of 2abc − ab − bc − ca.
Write the locus of a point the sum of whose distances from the coordinates axes is unity.
L is a variable line such that the algebraic sum of the distances of the points (1, 1), (2, 0) and (0, 2) from the line is equal to zero. The line L will always pass through
The distance between the orthocentre and circumcentre of the triangle with vertices (1, 2), (2, 1) and \[\left( \frac{3 + \sqrt{3}}{2}, \frac{3 + \sqrt{3}}{2} \right)\] is
The line segment joining the points (1, 2) and (−2, 1) is divided by the line 3x + 4y = 7 in the ratio ______.
The value of λ for which the lines 3x + 4y = 5, 5x + 4y = 4 and λx + 4y = 6 meet at a point is
Show that the locus of the mid-point of the distance between the axes of the variable line x cosα + y sinα = p is `1/x^2 + 1/y^2 = 4/p^2` where p is a constant.
The distance of the point P(1, – 3) from the line 2y – 3x = 4 is ______.
A point moves such that its distance from the point (4, 0) is half that of its distance from the line x = 16. The locus of the point is ______.
If the sum of the distances of a moving point in a plane from the axes is 1, then find the locus of the point.
The distance between the lines y = mx + c1 and y = mx + c2 is ______.
A point equidistant from the lines 4x + 3y + 10 = 0, 5x – 12y + 26 = 0 and 7x + 24y – 50 = 0 is ______.
A point moves so that square of its distance from the point (3, –2) is numerically equal to its distance from the line 5x – 12y = 3. The equation of its locus is ______.
The value of the λ, if the lines (2x + 3y + 4) + λ (6x – y + 12) = 0 are
| Column C1 | Column C2 |
| (a) Parallel to y-axis is | (i) λ = `-3/4` |
| (b) Perpendicular to 7x + y – 4 = 0 is | (ii) λ = `-1/3` |
| (c) Passes through (1, 2) is | (iii) λ = `-17/41` |
| (d) Parallel to x axis is | λ = 3 |
The point of intersection of the diagonals of the rectangle whose sides are contained in the lines x = 8, x = 10, y = 11, and y =12 is
The distance between the parallel lines 3x − 4y + 7 = 0 and 3x − 4y + 5 = 0 is `a/b`. Value of a + b is ______.
