Advertisements
Advertisements
प्रश्न
A rod of length 12 m moves with its ends always touching the coordinate axes. Determine the equation of the locus of a point P on the rod, which is 3 cm from the end in contact with x-axis.
उत्तर
Let AB be the rod making an angle θ with OX and let P (x, y) be the point on it such that AP = 3 cm.
Then, PB = AB – AP = (12 – 3) cm = 9 cm [∵ AB = 12 cm]
From P, draw PQ⊥OY and PR⊥OX.
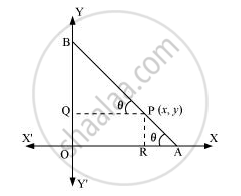
\[\text{ In } \bigtriangleup PBQ, \text{ we have }: \]
\[\cos \theta = \frac{PQ}{PB} = \frac{x}{9}\]
\[\text{ In } \bigtriangleup PRA, \text{ we have }: \]
\[\sin \theta = \frac{PR}{PA} = \frac{y}{3}\]
\[\text{ Since } \sin^2 \theta + \cos^2 \theta = 1, \text{ we have }: \]
\[ \left( \frac{y}{3} \right)^2 + \left( \frac{x}{9} \right)^2 = 1\]
\[ \Rightarrow \frac{x^2}{81} + \frac{y^2}{9} = 1\]
\[\text{ Thus, the locus of a point P on the rod is } \frac{x^2}{81} + \frac{y^2}{9} = 1 .\]
APPEARS IN
संबंधित प्रश्न
Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.
`x^2/4 + y^2/25 = 1`
Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.
`x^2/16 + y^2/9 = 1`
Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.
`x^2/25 + y^2/100 = 1`
Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.
`x^2/49 + y^2/36 = 1`
Find the vertex, focus, axis, directrix and latus-rectum of the following parabola:
y2 = 8x
Find the vertex, focus, axis, directrix and latus-rectum of the following parabolas
y2 − 4y − 3x + 1 = 0
Find the vertex, focus, axis, directrix and latus-rectum of the following parabola
y2 − 4y + 4x = 0
Find the vertex, focus, axis, directrix and latus-rectum of the following parabola
y2 + 4x + 4y − 3 = 0
Find the vertex, focus, axis, directrix and latus-rectum of the following parabola
y2 = 8x + 8y
Write the axis of symmetry of the parabola y2 = x.
Write the distance between the vertex and focus of the parabola y2 + 6y + 2x + 5 = 0.
Write the coordinates of the vertex of the parabola whose focus is at (−2, 1) and directrix is the line x + y − 3 = 0.
If the coordinates of the vertex and focus of a parabola are (−1, 1) and (2, 3) respectively, then write the equation of its directrix.
In the parabola y2 = 4ax, the length of the chord passing through the vertex and inclined to the axis at π/4 is
The directrix of the parabola x2 − 4x − 8y + 12 = 0 is
Find the centre, the lengths of the axes, eccentricity, foci of the following ellipse:
x2 + 2y2 − 2x + 12y + 10 = 0
Find the centre, the lengths of the axes, eccentricity, foci of the following ellipse:
4x2 + y2 − 8x + 2y + 1 = 0
Find the centre, the lengths of the axes, eccentricity, foci of the following ellipse:
4x2 + 16y2 − 24x − 32y − 12 = 0
Write the eccentricity of the ellipse 9x2 + 5y2 − 18x − 2y − 16 = 0.
Given the ellipse with equation 9x2 + 25y2 = 225, find the major and minor axes, eccentricity, foci and vertices.
Find the equation of the ellipse with foci at (± 5, 0) and x = `36/5` as one of the directrices.
The equation of the circle having centre (1, –2) and passing through the point of intersection of the lines 3x + y = 14 and 2x + 5y = 18 is ______.
The equation of the ellipse whose centre is at the origin and the x-axis, the major axis, which passes through the points (–3, 1) and (2, –2) is ______.
The equation of the circle which passes through the point (4, 5) and has its centre at (2, 2) is ______.
If the lines 3x – 4y + 4 = 0 and 6x – 8y – 7 = 0 are tangents to a circle, then find the radius of the circle.
Find the equation of a circle which touches both the axes and the line 3x – 4y + 8 = 0 and lies in the third quadrant.
Find the distance between the directrices of the ellipse `x^2/36 + y^2/20` = 1
The shortest distance from the point (2, –7) to the circle x2 + y2 – 14x – 10y – 151 = 0 is equal to 5.
