Advertisements
Advertisements
प्रश्न
A tiling or tessellation of a flat surface is the covering of a plane using one or more geometric shapes, called tiles, with no overlaps and no gaps. Historically, tessellations were used in ancient Rome and in Islamic art. You may find tessellation patterns on floors, walls, paintings etc. Shown below is a tiled floor in the archaeological Museum of Seville, made using squares, triangles and hexagons.

A craftsman thought of making a floor pattern after being inspired by the above design. To ensure accuracy in his work, he made the pattern on the Cartesian plane. He used regular octagons, squares and triangles for his floor tessellation pattern
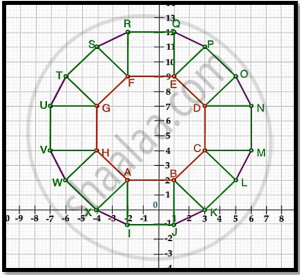
Use the above figure to answer the questions that follow:
- What is the length of the line segment joining points B and F?
- The centre ‘Z’ of the figure will be the point of intersection of the diagonals of quadrilateral WXOP. Then what are the coordinates of Z?
- What are the coordinates of the point on y-axis equidistant from A and G?
OR
What is the area of Trapezium AFGH?
उत्तर
i. B(1, 2), F(–2,9)
BF2 = (–2 –1)2 + (9 – 2)2
= (–3)2 + (7)2
= 9 + 49
= 58
So, BF = `sqrt(58)` units
ii.
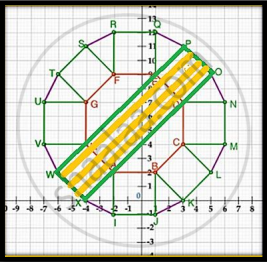
W(–6, 2), X(–4, 0), O(5, 9), P(3, 11)
Clearly, WXOP is a rectangle
The point of intersection of the diagonals of a rectangle is the midpoint of the diagonals. So the required point is the mid point of WO or XP.
= `((-6 + 5)/2, (2 + 9)/2)`
= `((-1)/2, 11/2)`
iii. A(–2, 2), G(–4, 7)
Let the point on y-axis be Z(0, y)
AZ2 = GZ2
(0 + 2)2 + (y – 2)2 = (0 + 4)2 + (y – 7)2
( 2)2 + y2 + 4 – 4y = (4)2 + y2 + 49 – 14y
8 – 4y = 65 – 14y
10y = 57
So, y = 5.7
i.e. the required point is (0, 5.7)
OR
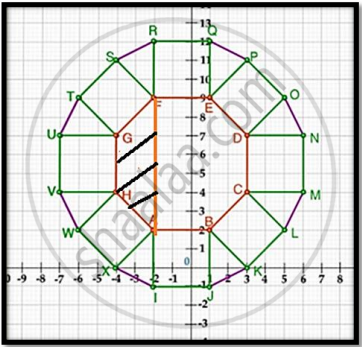
A(–2, 2), F(–2, 9), G(–4, 7), H(–4, 4)
Clearly GH = 7 – 4 = 3 units
AF = 9 – 2 = 7 units
So, height of the trapezium AFGH = 2 units
So, area of AFGH = `1/2`(AF + GH) × height
= `1/2`(7 + 3) × 2
= 10 sq.units
APPEARS IN
संबंधित प्रश्न
A line intersects the y-axis and x-axis at the points P and Q respectively. If (2, –5) is the mid-point of PQ, then find the coordinates of P and Q.
If the points A(k + 1, 2k), B(3k, 2k + 3) and C(5k − 1, 5k) are collinear, then find the value of k
If A(–2, 1), B(a, 0), C(4, b) and D(1, 2) are the vertices of a parallelogram ABCD, find the values of a and b. Hence find the lengths of its sides
Prove that the points (0, 0), (5, 5) and (-5, 5) are the vertices of a right isosceles triangle.
Determine the ratio in which the point P (m, 6) divides the join of A(-4, 3) and B(2, 8). Also, find the value of m.
Determine the ratio in which the point (-6, a) divides the join of A (-3, 1) and B (-8, 9). Also, find the value of a.
If the poin A(0,2) is equidistant form the points B (3, p) and C (p ,5) find the value of p. Also, find the length of AB.
The line segment joining the points A(3,−4) and B(1,2) is trisected at the points P(p,−2) and Q `(5/3,q)`. Find the values of p and q.
Find the area of quadrilateral ABCD whose vertices are A(-3, -1), B(-2,-4) C(4,-1) and D(3,4)
If the point A(0,2) is equidistant from the points B(3,p) and C(p, 5), find p.
The abscissa and ordinate of the origin are
If points Q and reflections of point P (−3, 4) in X and Y axes respectively, what is QR?
What is the distance between the points \[A\left( \sin\theta - \cos\theta, 0 \right)\] and \[B\left( 0, \sin\theta + \cos\theta \right)\] ?
The distance between the points (cos θ, 0) and (sin θ − cos θ) is
If the points (k, 2k), (3k, 3k) and (3, 1) are collinear, then k
If (−1, 2), (2, −1) and (3, 1) are any three vertices of a parallelogram, then
The point on the x-axis which is equidistant from points (−1, 0) and (5, 0) is
If point P is midpoint of segment joining point A(– 4, 2) and point B(6, 2), then the coordinates of P are ______
The line segment joining the points (3, -1) and (-6, 5) is trisected. The coordinates of point of trisection are ______.
If the coordinate of point A on the number line is –1 and that of point B is 6, then find d(A, B).
