Advertisements
Advertisements
प्रश्न
A uniform chain of mass m and length l overhangs a table with its two third part on the table. Find the work to be done by a person to put the hanging part back on the table.
उत्तर
Let 'dx' be the length of an element at distance x from the table.
Mass of the element, 'dm' \[= \left( \frac{\text{ m }}{\text{ l }} \right) \text{ dx }\]
Work done to putting back this mass element on the table is \[\text{ dW }= \left( \frac{\text{ m}}{\text{l}} \right) \times \text{ x } \times \text{ g } \times \text{ dx } \]
So, total work done to put \[\frac{1}{3}\] part back on the table
\[W = \int_0^{1/3} \left( \frac{\text{m}}{\text{l}} \right) \text{ gx dx }\]
\[ \Rightarrow \text{W} = \left( \frac{\text{m}}{\text{l}} \right) \text{g} \left[ \frac{x^2}{2} \right]^{1/3} \]
\[ = \frac{\text{mgl}}{18 \text{l}} = \frac{\text{mgl}}{18}\]
The work to be done by a person to put the hanging part back on the table is \[\frac{\text{ mgl } }{18}\] .
APPEARS IN
संबंधित प्रश्न
Figure shows a cart. Complete the table shown below.
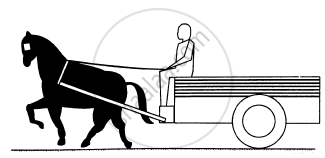
| Force on | Force by | Nature of the Force | Direction |
| Cart |
1 |
||
| Horse |
1 |
||
| Driver |
1 |
Mark the correct statements :
(a) The nuclear force between two protons is always greater than the electromagnetic force between them.
(b) The electromagnetic force between two protons is always greater than the gravitational force between them.
(c) The gravitational force between two protons may be greater than the nuclear force between them.
(d) Electromagnetic force between two protons may be greater than the nuclear force acting between them.
A monkey is sitting on a tree limb. The limb exerts a normal force of 48 N and a frictional force of 20 N. Find the magnitude of the total force exerted by the limb on the monkey.
Two charged particles placed at a separation of 20 cm exert 20 N of Coulomb force on each other. What will be the force of the separation is increased to 25 cm?
The force with which the earth attracts an object is called the weight of the object. Calculate the weight of the moon from the following data : The universal constant of gravitation G = 6.67 × 11−11 N−m2/kg2, mass of the moon = 7.36 × 1022 kg, mass of the earth = 6 × 1024 kg and the distance between the earth and the moon = 3.8 × 105 km.
In tug of war, the team that exerts a larger tangential force on the ground wins. Consider the period in which a team is dragging the opposite team by applying a larger tangential force on the ground. List which of the following works are positive, which are negative and which are zero?
(a) work by the winning team on the losing team
(b) work by the losing team on the winning team
(c) work by the ground on the winning team
(d) work by the ground on the losing team
(e) total external work on the two teams.
The work done by all the forces (external and internal) on a system equals the change in ______.
A constant force of 2⋅5 N accelerates a stationary particle of mass 15 g through a displacement of 2⋅5 m. Find the work done and the average power delivered.
A force \[F = \alpha + bx\] acts on a particle in the x-direction, where a and b are constants. Find the work done by this force during a displacement from x = 0 to x = d.
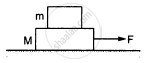
A block of mass m is kept over another block of mass M and the system rests on a horizontal surface (In the following figure). A constant horizontal force F acting on the lower block produces an acceleration \[\frac{F}{2 \left( m + M \right)}\] in the system, and the two blocks always move together. (a) Find the coefficient of kinetic friction between the bigger block and the horizontal surface. (b) Find the frictional force acting on the smaller block. (c) Find the work done by the force of friction on the smaller block by the bigger block during a displacement d of the system.
A particle of mass m moves on a straight line with its velocity varying with the distance travelled, according to the equation \[\nu = a\sqrt{x}\] , where a is a constant. Find the total work done by all the forces during a displacement from \[x = 0 \text{ to } x - d\] .
The 200 m free-style women's swimming gold medal at Seoul Olympics in 1988 was won by Heike Friendrich of East Germany when she set a new Olympic record of 1 minute and 57⋅56 seconds. Assume that she covered most of the distance with a uniform speed and had to exert 460 W to maintain her speed. Calculate the average force of resistance offered by the water during the swim.
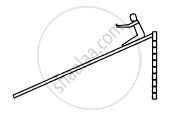
In a children's park, there is a slide which has a total length of 10 m and a height of 8⋅0 m . A vertical ladder is provided to reach the top. A boy weighing 200 N climbs up the ladder to the top of the slide and slides down to the ground. The average friction offered by the slide is three tenth of his weight. Find (a) the work done by the ladder on the boy as he goes up; (b) the work done by the slide on the boy as he comes down. Neglect any work done by forces inside the body of the boy
A lawn roller is pulled along a horizontal surface through a distance of 20 m by a rope with a force of 200 N. If the rope makes an angle of 60° with the vertical while pulling, the amount of work done by the pulling force is:
A body is moving unidirectionally under the influence of a source of constant power supplying energy. Which of the diagrams shown in figure correctly shows the displacement-time curve for its motion?
A body is being raised to a height h from the surface of earth. What is the sign of work done by gravitational force?
A block of mass 1 kg is pushed up a surface inclined to horizontal at an angle of 30° by a force of 10 N parallel to the inclined surface (Figure). The coefficient of friction between block and the incline is 0.1. If the block is pushed up by 10 m along the incline, calulate
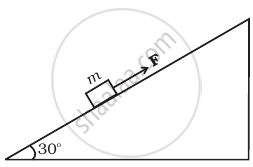
- work done against gravity
- work done against force of friction
- increase in potential energy
- increase in kinetic energy
- work done by applied force.
