Advertisements
Advertisements
प्रश्न
A uniform chain of mass m and length l overhangs a table with its two third part on the table. Find the work to be done by a person to put the hanging part back on the table.
उत्तर
Let 'dx' be the length of an element at distance x from the table.
Mass of the element, 'dm' \[= \left( \frac{\text{ m }}{\text{ l }} \right) \text{ dx }\]
Work done to putting back this mass element on the table is \[\text{ dW }= \left( \frac{\text{ m}}{\text{l}} \right) \times \text{ x } \times \text{ g } \times \text{ dx } \]
So, total work done to put \[\frac{1}{3}\] part back on the table
\[W = \int_0^{1/3} \left( \frac{\text{m}}{\text{l}} \right) \text{ gx dx }\]
\[ \Rightarrow \text{W} = \left( \frac{\text{m}}{\text{l}} \right) \text{g} \left[ \frac{x^2}{2} \right]^{1/3} \]
\[ = \frac{\text{mgl}}{18 \text{l}} = \frac{\text{mgl}}{18}\]
The work to be done by a person to put the hanging part back on the table is \[\frac{\text{ mgl } }{18}\] .
APPEARS IN
संबंधित प्रश्न
A boy is sitting on a chair placed on the floor of a room. Write as many action-reaction pairs of forces as you can.
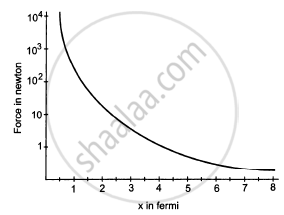
Suppose the magnitude of Nuclear force between two protons varies with the distance between them as shown in figure. Estimate the ratio "Nuclear force/Coulomb force" for
(a) x = 8 fm
(b) x = 4 fm
(c) x = 2 fm
(d) x = 1 fm (1 fm = 10 −15m).
Let E, G and N represent the magnitudes of electromagnetic gravitational and nuclear forces between two electrons at a given separation. Then
Mark the correct statements :
(a) The nuclear force between two protons is always greater than the electromagnetic force between them.
(b) The electromagnetic force between two protons is always greater than the gravitational force between them.
(c) The gravitational force between two protons may be greater than the nuclear force between them.
(d) Electromagnetic force between two protons may be greater than the nuclear force acting between them.
The gravitational force acting on a particle of 1 g due to a similar particle is equal to 6.67 × 10−17 N. Calculate the separation between the particles.
At what distance should two charges, each equal to 1 C, be placed so that the force between them equals your weight ?
Two charged particles placed at a separation of 20 cm exert 20 N of Coulomb force on each other. What will be the force of the separation is increased to 25 cm?
The average separation between the proton and the electron in a hydrogen atom in ground state is 5.3 × 10−11 m. (a) Calculate the Coulomb force between them at this separation. (b) When the atom goes into its first excited state the average separation between the proton and the electron increases to four times its value in the ground state. What is the Coulomb force in this state?
A small block of mass m is kept on a rough inclined surface of inclination θ fixed in an elevator. the elevator goes up with a uniform velocity v and the block does not slide on the wedge. The work done by the force of friction on the block in time t will be
A block of mass m slides down a smooth vertical circular track. During the motion, the block is in
A particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the plane. The motion of the particle takes place in a plane. It follows that
(a) its velocity is constant
(b) its acceleration is constant
(c) its kinetic energy is constant
(d) it moves in a circular path.
A block of mass 250 g slides down an incline of inclination 37° with uniform speed. Find the work done against friction as the block slides through 1m.
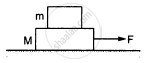
A block of mass m is kept over another block of mass M and the system rests on a horizontal surface (In the following figure). A constant horizontal force F acting on the lower block produces an acceleration \[\frac{F}{2 \left( m + M \right)}\] in the system, and the two blocks always move together. (a) Find the coefficient of kinetic friction between the bigger block and the horizontal surface. (b) Find the frictional force acting on the smaller block. (c) Find the work done by the force of friction on the smaller block by the bigger block during a displacement d of the system.
A block of mass 2.0 kg is pushed down an inclined plane of inclination 37° with a force of 20 N acting parallel to the incline. It is found that the block moves on the incline with an acceleration of 10 m/s2. If the block started from rest, find the work done (a) by the applied force in the first second, (b) by the weight of the block in the first second and (c) by the frictional force acting on the block in the first second. Take g = 10 m/s2.
A 250 g block slides on a rough horizontal table. Find the work done by the frictional force in bringing the block to rest if it is initially moving at a speed of 40 cm/s. If the friction coefficient between the table and the block is 0⋅1, how far does the block move before coming to rest?
The 200 m free-style women's swimming gold medal at Seoul Olympics in 1988 was won by Heike Friendrich of East Germany when she set a new Olympic record of 1 minute and 57⋅56 seconds. Assume that she covered most of the distance with a uniform speed and had to exert 460 W to maintain her speed. Calculate the average force of resistance offered by the water during the swim.
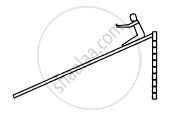
In a children's park, there is a slide which has a total length of 10 m and a height of 8⋅0 m . A vertical ladder is provided to reach the top. A boy weighing 200 N climbs up the ladder to the top of the slide and slides down to the ground. The average friction offered by the slide is three tenth of his weight. Find (a) the work done by the ladder on the boy as he goes up; (b) the work done by the slide on the boy as he comes down. Neglect any work done by forces inside the body of the boy
The work done by an applied variable force, F = x + x3 from x = 0 m to x = 2m, where x is displacement, is:
A bicyclist comes to a skidding stop in 10 m. During this process, the force on the bicycle due to the road is 200 N and is directly opposed to the motion. The work done by the cycle on the road is ______.
