Advertisements
Advertisements
प्रश्न
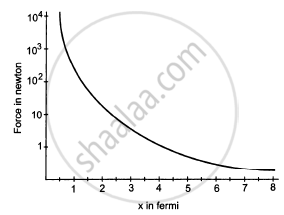
Suppose the magnitude of Nuclear force between two protons varies with the distance between them as shown in figure. Estimate the ratio "Nuclear force/Coulomb force" for
(a) x = 8 fm
(b) x = 4 fm
(c) x = 2 fm
(d) x = 1 fm (1 fm = 10 −15m).
उत्तर
First let us calculate the coulomb force between 2 protons for distance = 8 fm\[F = \frac{K q^2}{r^2}\]
\[ = \frac{9 \times {10}^9 \times (1 . 6 \times {10}^{- 19} )^2}{(8 \times {10}^{- 15} )^2}\]
\[ = 3 . 6 N\]
\[F_N = 0 . 05 N\]
\[\frac{F_N}{F_C} = \frac{0 . 05}{3 . 6} = 0 . 0138 N\]
For x= 4 fm
\[F_C = \frac{9 \times {10}^9 \times (1 . 6 \times {10}^{- 19} )^2}{(4 \times {10}^{- 15} )^2}\]
\[ = \frac{23 . 04 \times {10}^{- 29}}{(4 \times {10}^{- 15} )^2}\]
\[ = 14 . 4 N\]
\[ F_N = 1N\]
\[\frac{F_N}{F_C} = \frac{1}{14 . 4} = 0 . 0694 N\]
\[\text{ For }\ x = 2 \text{ fm } \]
\[ F_C = \frac{9 \times {10}^9 \times (1 . 6 \times {10}^{- 19} )^2}{(2 \times {10}^{- 15} )^2}\]
\[ = 57 . 6 N\]
\[ F_N = 10 N\]
\[\frac{F_N}{F_C} = \frac{10}{57 . 6} = 0 . 173\]
\[\text{ For }\ x = 1 \text{ fm } \]
\[ F_C = \frac{9 \times {10}^9 \times (1 . 6 \times {10}^{- 19} )^2}{(1 \times {10}^{- 15} )^2}\]
\[ = 230 . 4 N\]
\[ F_N = 1000 N\]
\[\frac{F_N}{F_C} = \frac{1000}{230 . 4} = 4 . 34\]
APPEARS IN
संबंधित प्रश्न
State if the following statement is true or false. Give a reason for your answer.
Work done in the motion of a body over a closed loop is zero for every force in nature.
A neutron exerts a force on a proton which is
(a) gravitational
(b) electromagnetic
(c) nuclear
(d) weak
A proton exerts a force on a proton which is
(a) gravitational
(b) electromagnetic
(c) nuclear
(d) weak
The gravitational force acting on a particle of 1 g due to a similar particle is equal to 6.67 × 10−17 N. Calculate the separation between the particles.
The work done by the external forces on a system equals the change in
The work done by all the forces (external and internal) on a system equals the change in ______.
A block of mass 5.0 kg slides down an incline of inclination 30° and length 10 m. Find the work done by the force of gravity.
A man moves on a straight horizontal road with a block of mass 2 kg in his hand. If he covers a distance of 40 m with an acceleration of 0⋅5 m/s2, find the work done by the man on the block during the motion.
A box weighing 2000 N is to be slowly slid through 20 m on a straight track with friction coefficient 0⋅2 with the box. (a) Find the work done by the person pulling the box with a chain at an angle θ with the horizontal. (b) Find the work when the person has chosen a value of θ, which ensures him the minimum magnitude of the force.
A particle of mass m moves on a straight line with its velocity varying with the distance travelled, according to the equation \[\nu = a\sqrt{x}\] , where a is a constant. Find the total work done by all the forces during a displacement from \[x = 0 \text{ to } x - d\] .
A block of mass 2.0 kg is pushed down an inclined plane of inclination 37° with a force of 20 N acting parallel to the incline. It is found that the block moves on the incline with an acceleration of 10 m/s2. If the block started from rest, find the work done (a) by the applied force in the first second, (b) by the weight of the block in the first second and (c) by the frictional force acting on the block in the first second. Take g = 10 m/s2.
Water falling from a 50-m high fall is to be used for generating electric energy. If \[1 \cdot 8 \times {10}^5 \text{ kg } \] of water falls per hour and half the gravitational potential energy can be converted into electrical energy, how many 100 W lamps can be lit with the generated energy?
A particle of mass m is kept on a fixed, smooth sphere of radius R at a position where the radius through the particle makes an angle of 30° with the vertical. The particle is released from this position. (a) What is the force exerted by the sphere on the particle just after the release? (b) Find the distance travelled by the particle before it loses contact with the sphere.
A force F = 20 + 10y acts on a particle in y-direction where F is in newton and y in metre. Work done by this force to move the particle from y – 0 to y – 1 m is:
A lawn roller is pulled along a horizontal surface through a distance of 20 m by a rope with a force of 200 N. If the rope makes an angle of 60° with the vertical while pulling, the amount of work done by the pulling force is:
A bicyclist comes to a skidding stop in 10 m. During this process, the force on the bicycle due to the road is 200 N and is directly opposed to the motion. The work done by the cycle on the road is ______.
A body of mass 0.5 kg travels in a straight line with velocity v = a x3/2 where a = 5 m–1/2s–1. The work done by the net force during its displacement from x = 0 to x = 2 m is ______.
A body is moving unidirectionally under the influence of a source of constant power supplying energy. Which of the diagrams shown in figure correctly shows the displacement-time curve for its motion?
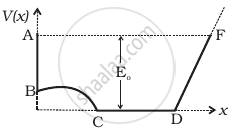
A graph of potential energy V(x) verses x is shown in figure. A particle of energy E0 is executing motion in it. Draw graph of velocity and kinetic energy versus x for one complete cycle AFA.
A body is displaced from (0, 0) to (1 m, 1 m) along the path x = y by a force F = (x2`hat"J"` + y`hat"i"`)N. The work done by this force will be:
