Advertisements
Advertisements
प्रश्न
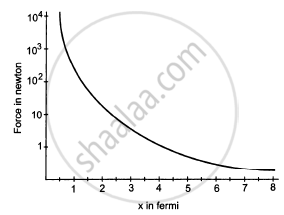
Suppose the magnitude of Nuclear force between two protons varies with the distance between them as shown in figure. Estimate the ratio "Nuclear force/Coulomb force" for
(a) x = 8 fm
(b) x = 4 fm
(c) x = 2 fm
(d) x = 1 fm (1 fm = 10 −15m).
उत्तर
First let us calculate the coulomb force between 2 protons for distance = 8 fm\[F = \frac{K q^2}{r^2}\]
\[ = \frac{9 \times {10}^9 \times (1 . 6 \times {10}^{- 19} )^2}{(8 \times {10}^{- 15} )^2}\]
\[ = 3 . 6 N\]
\[F_N = 0 . 05 N\]
\[\frac{F_N}{F_C} = \frac{0 . 05}{3 . 6} = 0 . 0138 N\]
For x= 4 fm
\[F_C = \frac{9 \times {10}^9 \times (1 . 6 \times {10}^{- 19} )^2}{(4 \times {10}^{- 15} )^2}\]
\[ = \frac{23 . 04 \times {10}^{- 29}}{(4 \times {10}^{- 15} )^2}\]
\[ = 14 . 4 N\]
\[ F_N = 1N\]
\[\frac{F_N}{F_C} = \frac{1}{14 . 4} = 0 . 0694 N\]
\[\text{ For }\ x = 2 \text{ fm } \]
\[ F_C = \frac{9 \times {10}^9 \times (1 . 6 \times {10}^{- 19} )^2}{(2 \times {10}^{- 15} )^2}\]
\[ = 57 . 6 N\]
\[ F_N = 10 N\]
\[\frac{F_N}{F_C} = \frac{10}{57 . 6} = 0 . 173\]
\[\text{ For }\ x = 1 \text{ fm } \]
\[ F_C = \frac{9 \times {10}^9 \times (1 . 6 \times {10}^{- 19} )^2}{(1 \times {10}^{- 15} )^2}\]
\[ = 230 . 4 N\]
\[ F_N = 1000 N\]
\[\frac{F_N}{F_C} = \frac{1000}{230 . 4} = 4 . 34\]
APPEARS IN
संबंधित प्रश्न
State if the following statement is true or false. Give a reason for your answer.
Work done in the motion of a body over a closed loop is zero for every force in nature.
A body constrained to move along the z-axis of a coordinate system is subject to a constant force F given by
`F = -hati+2hatj+3hatkN`
Where `hati,hatj,hatk` are unit vectors along the x-, y- and z-axis of the system respectively. What is the work done by this force in moving the body a distance of 4 m along the z-axis ?
Is it true that the reaction of a gravitational force is always gravitational, of an electromagnetic force is always electromagnetic and so on?
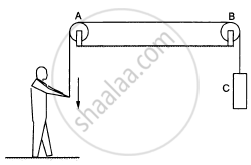
List all the forces acting on (a) the pulley A, (b) the boy and (c) the block C in figure.
A neutron exerts a force on a proton which is
(a) gravitational
(b) electromagnetic
(c) nuclear
(d) weak
The gravitational force acting on a particle of 1 g due to a similar particle is equal to 6.67 × 10−17 N. Calculate the separation between the particles.
The force with which the earth attracts an object is called the weight of the object. Calculate the weight of the moon from the following data : The universal constant of gravitation G = 6.67 × 11−11 N−m2/kg2, mass of the moon = 7.36 × 1022 kg, mass of the earth = 6 × 1024 kg and the distance between the earth and the moon = 3.8 × 105 km.
The work done by the external forces on a system equals the change in
No work is done by a force on an object if
(a) the force is always perpendicular to its velocity
(b) the force is always perpendicular to its acceleration
(c) the object is stationary but the point of application of the force moves on the object
(d) the object moves in such a way that the point of application of the force remains fixed.
A man moves on a straight horizontal road with a block of mass 2 kg in his hand. If he covers a distance of 40 m with an acceleration of 0⋅5 m/s2, find the work done by the man on the block during the motion.
A block of weight 100 N is slowly moved up a smooth incline of inclination 37° by a person. Calculate the work done by the person in moving the block through a distance of 2 m, if the driving force is (a) parallel to the incline and (b) in the horizontal direction.
Find the average frictional force needed to stop a car weighing 500 kg at a distance of 25 m if the initial speed is 72 km/h.
A particle of mass m moves on a straight line with its velocity varying with the distance travelled, according to the equation \[\nu = a\sqrt{x}\] , where a is a constant. Find the total work done by all the forces during a displacement from \[x = 0 \text{ to } x - d\] .
A block of mass 2 kg kept at rest on an inclined plane of inclination 37° is pulled up the plane by applying a constant force of 20 N parallel to the incline. The force acts for one second. Find the work done by the force of gravity in that one second if the work done by the applied force is 40 J.
A block of mass 2 kg kept at rest on an inclined plane of inclination 37° is pulled up the plane by applying a constant force of 20 N parallel to the incline. The force acts for one second. Find the kinetic energy of the block at the instant the force ceases to act. Take g = 10 m/s2.
The 200 m free-style women's swimming gold medal at Seoul Olympics in 1988 was won by Heike Friendrich of East Germany when she set a new Olympic record of 1 minute and 57⋅56 seconds. Assume that she covered most of the distance with a uniform speed and had to exert 460 W to maintain her speed. Calculate the average force of resistance offered by the water during the swim.
A uniform chain of length L and mass M overhangs a horizontal table with its two third part on the table. The friction coefficient between the table and the chain is μ . Find the work done by friction during the period the chain slips off the table.
The work done by an applied variable force, F = x + x3 from x = 0 m to x = 2m, where x is displacement, is:
Work done by gas in cyclic process is ______ J.