Advertisements
Advertisements
प्रश्न
A uniform chain of length L and mass M overhangs a horizontal table with its two third part on the table. The friction coefficient between the table and the chain is μ . Find the work done by friction during the period the chain slips off the table.
उत्तर
Let x length of the chain be on the table at a particular instant.
Consider a small element of length 'dx' and mass 'dm' on the table.
dm = \[\frac{M}{L}\text{ dx}\] Work done by the friction on this element is \[\text{ dW }= \mu \text{ Rx } = \mu \left( \frac{M}{L} \times \text{ gx } \right) \text{ dx }\]
Total work done by friction on two third part of the chain,
\[W = \int_{2L/3}^0 \mu\frac{M}{L} \text{ gx dx }\]
\[ \therefore W = \mu\frac{M}{L}\text{ g } \left[ \frac{\text{x}^2}{2} \right]_0^{2\text{L}/3} \]
\[ = - \mu\frac{M}{L}\text{g} \left[ \frac{4 L^2}{18} \right]\]
\[ = - \frac{2\mu \text{ MgL} }{9}\]
The total work done by friction during the period the chain slips off the table is \[- \frac{2\mu \text{ MgL }}{9}\]
APPEARS IN
संबंधित प्रश्न
A body constrained to move along the z-axis of a coordinate system is subject to a constant force F given by
`F = -hati+2hatj+3hatkN`
Where `hati,hatj,hatk` are unit vectors along the x-, y- and z-axis of the system respectively. What is the work done by this force in moving the body a distance of 4 m along the z-axis ?
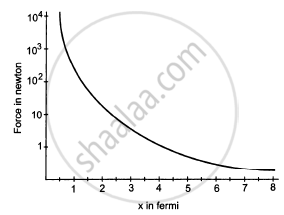
Suppose the magnitude of Nuclear force between two protons varies with the distance between them as shown in figure. Estimate the ratio "Nuclear force/Coulomb force" for
(a) x = 8 fm
(b) x = 4 fm
(c) x = 2 fm
(d) x = 1 fm (1 fm = 10 −15m).
Let E, G and N represent the magnitudes of electromagnetic gravitational and nuclear forces between two electrons at a given separation. Then
A 60 kg man pushes a 40 kg man by a force of 60 N. The 40 kg man has pushed the other man with a force of
A neutron exerts a force on a proton which is
(a) gravitational
(b) electromagnetic
(c) nuclear
(d) weak
The gravitational force acting on a particle of 1 g due to a similar particle is equal to 6.67 × 10−17 N. Calculate the separation between the particles.
A monkey is sitting on a tree limb. The limb exerts a normal force of 48 N and a frictional force of 20 N. Find the magnitude of the total force exerted by the limb on the monkey.
A block of mass m slides down a smooth vertical circular track. During the motion, the block is in
A particle moves from a point \[\overrightarrow{r}_1 = \left( 2 m \right) \overrightarrow{ i } + \left( 3 m \right) \overrightarrow{ j } \] to another point
\[\overrightarrow{r}_2 = \left( 3 m \right) \overrightarrow{ i } + \left( 2 m \right) \overrightarrow{ j } \] acts on it. Find the work done by the force on the particle during the displacement.
A man moves on a straight horizontal road with a block of mass 2 kg in his hand. If he covers a distance of 40 m with an acceleration of 0⋅5 m/s2, find the work done by the man on the block during the motion.
A block of mass 250 g slides down an incline of inclination 37° with uniform speed. Find the work done against friction as the block slides through 1m.
A particle of mass m moves on a straight line with its velocity varying with the distance travelled, according to the equation \[\nu = a\sqrt{x}\] , where a is a constant. Find the total work done by all the forces during a displacement from \[x = 0 \text{ to } x - d\] .
A block of mass 2 kg kept at rest on an inclined plane of inclination 37° is pulled up the plane by applying a constant force of 20 N parallel to the incline. The force acts for one second. Show that the work done by the applied force does not exceed 40 J.
A bicyclist comes to a skidding stop in 10 m. During this process, the force on the bicycle due to the road is 200 N and is directly opposed to the motion. The work done by the cycle on the road is ______.
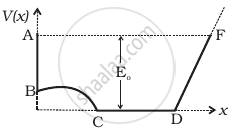
A graph of potential energy V(x) verses x is shown in figure. A particle of energy E0 is executing motion in it. Draw graph of velocity and kinetic energy versus x for one complete cycle AFA.
A block of mass 1 kg is pushed up a surface inclined to horizontal at an angle of 30° by a force of 10 N parallel to the inclined surface (Figure). The coefficient of friction between block and the incline is 0.1. If the block is pushed up by 10 m along the incline, calulate
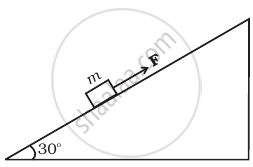
- work done against gravity
- work done against force of friction
- increase in potential energy
- increase in kinetic energy
- work done by applied force.
A block of mass m is taken from A to B slowly under the action of a constant force R Work done by this force is ______.

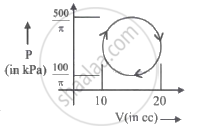
Work done by gas in cyclic process is ______ J.