Advertisements
Advertisements
प्रश्न
A particle of mass m is kept on a fixed, smooth sphere of radius R at a position where the radius through the particle makes an angle of 30° with the vertical. The particle is released from this position. (a) What is the force exerted by the sphere on the particle just after the release? (b) Find the distance travelled by the particle before it loses contact with the sphere.
उत्तर
(a) When the particle is released from rest, the centrifugal force is zero.
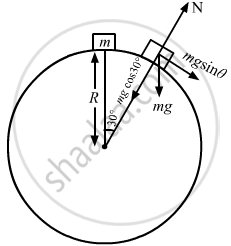
\[\text{N force = mg }\cos \theta = \text{ mg } \cos 30^\circ\]
\[ = \frac{\sqrt{3}}{2} \text{ mg }\]
(b) Consider that the particle loses contact with the surface at a point whose angle with the horizontal is θ .
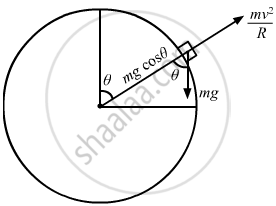
\[\text{So}, \frac{\text{m}\nu^2}{R} = \text{mg}\cos \theta\]
\[ \Rightarrow \nu^2 = \text{Rg} \cos \theta . . . (i)\]
\[\text{Again,} \left( \frac{1}{2} \right) \text{m} \nu^2 = \text{ mg }R \left( \cos 30^\circ- \cos \theta \right)\]
\[ \Rightarrow \nu^2 = 2\text{ Rg }\left( \frac{\sqrt{3}}{2} - \cos \theta \right) . . . (\text{ii})\]
From equations (i) and (ii),
\[ \Rightarrow \cos \theta = \frac{1}{\sqrt{3}}\]
\[\text{ or } \theta = \cos^{- 1} \frac{1}{\sqrt{3}}\]
\[L = R \left( \theta - \frac{\pi}{6} \right)\]
\[ \left[ \text{ because }30^\circ= \left( \frac{\pi}{6} \right) \right]\]
Putting the value of θ, we get:
L = 0.43 R
APPEARS IN
संबंधित प्रश्न
A body constrained to move along the z-axis of a coordinate system is subject to a constant force F given by
`F = -hati+2hatj+3hatkN`
Where `hati,hatj,hatk` are unit vectors along the x-, y- and z-axis of the system respectively. What is the work done by this force in moving the body a distance of 4 m along the z-axis ?
A body of mass m is placed on a table. The earth is pulling the body with a force mg. Taking this force to be the action what is the reaction?
A lawyer alleges in court that the police had forced his client to issue a statement of confession. What kind of force is this ?
Is it true that the reaction of a gravitational force is always gravitational, of an electromagnetic force is always electromagnetic and so on?
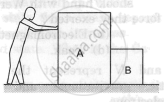
List all the forces acting on the block B in figure.
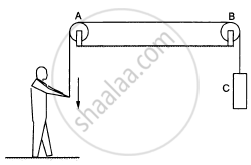
List all the forces acting on (a) the pulley A, (b) the boy and (c) the block C in figure.
Two charged particles placed at a separation of 20 cm exert 20 N of Coulomb force on each other. What will be the force of the separation is increased to 25 cm?
The work done by all the forces (external and internal) on a system equals the change in ______.
A small block of mass m is kept on a rough inclined surface of inclination θ fixed in an elevator. the elevator goes up with a uniform velocity v and the block does not slide on the wedge. The work done by the force of friction on the block in time t will be
A particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the plane. The motion of the particle takes place in a plane. It follows that
(a) its velocity is constant
(b) its acceleration is constant
(c) its kinetic energy is constant
(d) it moves in a circular path.
A box is pushed through 4.0 m across a floor offering 100 N resistance. How much work is done by the resisting force?
A force \[F = \alpha + bx\] acts on a particle in the x-direction, where a and b are constants. Find the work done by this force during a displacement from x = 0 to x = d.
A block of mass 250 g slides down an incline of inclination 37° with uniform speed. Find the work done against friction as the block slides through 1m.
A particle of mass m moves on a straight line with its velocity varying with the distance travelled, according to the equation \[\nu = a\sqrt{x}\] , where a is a constant. Find the total work done by all the forces during a displacement from \[x = 0 \text{ to } x - d\] .
A block of mass 2.0 kg is pushed down an inclined plane of inclination 37° with a force of 20 N acting parallel to the incline. It is found that the block moves on the incline with an acceleration of 10 m/s2. If the block started from rest, find the work done (a) by the applied force in the first second, (b) by the weight of the block in the first second and (c) by the frictional force acting on the block in the first second. Take g = 10 m/s2.
The 200 m free-style women's swimming gold medal at Seoul Olympics in 1988 was won by Heike Friendrich of East Germany when she set a new Olympic record of 1 minute and 57⋅56 seconds. Assume that she covered most of the distance with a uniform speed and had to exert 460 W to maintain her speed. Calculate the average force of resistance offered by the water during the swim.
The work done by an applied variable force, F = x + x3 from x = 0 m to x = 2m, where x is displacement, is:
A lawn roller is pulled along a horizontal surface through a distance of 20 m by a rope with a force of 200 N. If the rope makes an angle of 60° with the vertical while pulling, the amount of work done by the pulling force is:
A body of mass 0.5 kg travels in a straight line with velocity v = a x3/2 where a = 5 m–1/2s–1. The work done by the net force during its displacement from x = 0 to x = 2 m is ______.
