Advertisements
Advertisements
Question
A particle of mass m is kept on a fixed, smooth sphere of radius R at a position where the radius through the particle makes an angle of 30° with the vertical. The particle is released from this position. (a) What is the force exerted by the sphere on the particle just after the release? (b) Find the distance travelled by the particle before it loses contact with the sphere.
Solution
(a) When the particle is released from rest, the centrifugal force is zero.
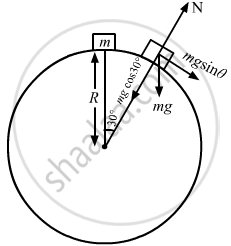
\[\text{N force = mg }\cos \theta = \text{ mg } \cos 30^\circ\]
\[ = \frac{\sqrt{3}}{2} \text{ mg }\]
(b) Consider that the particle loses contact with the surface at a point whose angle with the horizontal is θ .
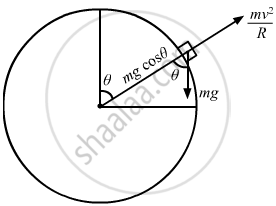
\[\text{So}, \frac{\text{m}\nu^2}{R} = \text{mg}\cos \theta\]
\[ \Rightarrow \nu^2 = \text{Rg} \cos \theta . . . (i)\]
\[\text{Again,} \left( \frac{1}{2} \right) \text{m} \nu^2 = \text{ mg }R \left( \cos 30^\circ- \cos \theta \right)\]
\[ \Rightarrow \nu^2 = 2\text{ Rg }\left( \frac{\sqrt{3}}{2} - \cos \theta \right) . . . (\text{ii})\]
From equations (i) and (ii),
\[ \Rightarrow \cos \theta = \frac{1}{\sqrt{3}}\]
\[\text{ or } \theta = \cos^{- 1} \frac{1}{\sqrt{3}}\]
\[L = R \left( \theta - \frac{\pi}{6} \right)\]
\[ \left[ \text{ because }30^\circ= \left( \frac{\pi}{6} \right) \right]\]
Putting the value of θ, we get:
L = 0.43 R
APPEARS IN
RELATED QUESTIONS
When you hold a pen and write on your notebook, what kind of force is exerted by you on the pen? By the pen on the notebook? By you on the notebook?
Is it true that the reaction of a gravitational force is always gravitational, of an electromagnetic force is always electromagnetic and so on?
A 60 kg man pushes a 40 kg man by a force of 60 N. The 40 kg man has pushed the other man with a force of
The gravitational force acting on a particle of 1 g due to a similar particle is equal to 6.67 × 10−17 N. Calculate the separation between the particles.
Two spherical bodies, each of mass 50 kg, are placed at a separation of 20 cm. Equal charges are placed on the bodies and it is found that the force of Coulomb repulsion equals the gravitational attraction in magnitude. Find the magnitude of the charge placed on either body.
The average separation between the proton and the electron in a hydrogen atom in ground state is 5.3 × 10−11 m. (a) Calculate the Coulomb force between them at this separation. (b) When the atom goes into its first excited state the average separation between the proton and the electron increases to four times its value in the ground state. What is the Coulomb force in this state?
In tug of war, the team that exerts a larger tangential force on the ground wins. Consider the period in which a team is dragging the opposite team by applying a larger tangential force on the ground. List which of the following works are positive, which are negative and which are zero?
(a) work by the winning team on the losing team
(b) work by the losing team on the winning team
(c) work by the ground on the winning team
(d) work by the ground on the losing team
(e) total external work on the two teams.
The magnetic force on a charged particle is always perpendicular to its velocity. Can the magnetic force change the velocity of the particles? Speed of the particle?
The work done by all the forces (external and internal) on a system equals the change in ______.
A constant force of 2⋅5 N accelerates a stationary particle of mass 15 g through a displacement of 2⋅5 m. Find the work done and the average power delivered.
A block of mass 250 g slides down an incline of inclination 37° with uniform speed. Find the work done against friction as the block slides through 1m.
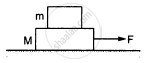
A block of mass m is kept over another block of mass M and the system rests on a horizontal surface (In the following figure). A constant horizontal force F acting on the lower block produces an acceleration \[\frac{F}{2 \left( m + M \right)}\] in the system, and the two blocks always move together. (a) Find the coefficient of kinetic friction between the bigger block and the horizontal surface. (b) Find the frictional force acting on the smaller block. (c) Find the work done by the force of friction on the smaller block by the bigger block during a displacement d of the system.
Find the average force needed to accelerate a car weighing 500 kg from rest to 72 km/h through a distance of 25 m.
A block of mass 2 kg kept at rest on an inclined plane of inclination 37° is pulled up the plane by applying a constant force of 20 N parallel to the incline. The force acts for one second. Find the kinetic energy of the block at the instant the force ceases to act. Take g = 10 m/s2.
A block of mass 2.0 kg is pushed down an inclined plane of inclination 37° with a force of 20 N acting parallel to the incline. It is found that the block moves on the incline with an acceleration of 10 m/s2. If the block started from rest, find the work done (a) by the applied force in the first second, (b) by the weight of the block in the first second and (c) by the frictional force acting on the block in the first second. Take g = 10 m/s2.
A 250 g block slides on a rough horizontal table. Find the work done by the frictional force in bringing the block to rest if it is initially moving at a speed of 40 cm/s. If the friction coefficient between the table and the block is 0⋅1, how far does the block move before coming to rest?
Water falling from a 50-m high fall is to be used for generating electric energy. If \[1 \cdot 8 \times {10}^5 \text{ kg } \] of water falls per hour and half the gravitational potential energy can be converted into electrical energy, how many 100 W lamps can be lit with the generated energy?
A bicyclist comes to a skidding stop in 10 m. During this process, the force on the bicycle due to the road is 200 N and is directly opposed to the motion. The work done by the cycle on the road is ______.
A body is being raised to a height h from the surface of earth. What is the sign of work done by applied force?
Force acting on a particle is (2`hat"i"` + 3 `hat"j"`) N. Work done by this force is zero, when a particle is moved on the line 3y + kx = 5. Here value of k is ______.
