Advertisements
Advertisements
Question
The average separation between the proton and the electron in a hydrogen atom in ground state is 5.3 × 10−11 m. (a) Calculate the Coulomb force between them at this separation. (b) When the atom goes into its first excited state the average separation between the proton and the electron increases to four times its value in the ground state. What is the Coulomb force in this state?
Solution
Average separation between the proton and the electron of a Hydrogen atom in ground state, r = 5.3 × 10−11 m
(a) Coulomb force when the proton and the electron in a hydrogen atom in ground state
\[F = 9 \times {10}^9 \times \frac{q_1 q_2}{r_2}\]
\[ = \frac{9 \times {10}^9 \times \left( 1 . 6 \times {10}^{- 19} \right)^2}{\left( 5 . 3 \times {10}^{- 11} \right)^2} = 8 . 2 \times {10}^{- 8} \text{N}\]
(b) Coulomb force when the average distance between the proton and the electron becomes 4 times that of its ground state
\[\text {Coulomb force, F } = \frac{1}{4\pi \in_0} = \frac{q_1 q_2}{\left( 4r \right)^2}\]
\[ = \frac{9 \times {10}^9 \times \left( 1 . 6 \times {10}^{- 19} \right)^2}{16 \times \left( 5 . 3 \right)^2 \times {10}^{- 22}}\]
\[ = \frac{9 \times \left( 1 . 6 \right)^2}{10 \times \left( 5 . 3 \right)^2} \times {10}^{- 7} \]
\[ = 0 . 0512 \times {10}^{- 7} \]
\[ = 5 . 1 \times {10}^{- 9} \text{ N }\]
APPEARS IN
RELATED QUESTIONS
The sum of all electromagnetic forces between different particles of a system of charged particles is zero
A neutron exerts a force on a proton which is
(a) gravitational
(b) electromagnetic
(c) nuclear
(d) weak
The gravitational force acting on a particle of 1 g due to a similar particle is equal to 6.67 × 10−17 N. Calculate the separation between the particles.
The force with which the earth attracts an object is called the weight of the object. Calculate the weight of the moon from the following data : The universal constant of gravitation G = 6.67 × 11−11 N−m2/kg2, mass of the moon = 7.36 × 1022 kg, mass of the earth = 6 × 1024 kg and the distance between the earth and the moon = 3.8 × 105 km.
Find the ratio of the magnitude of the electric force to the gravitational force acting between two protons.
A particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the plane. The motion of the particle takes place in a plane. It follows that
(a) its velocity is constant
(b) its acceleration is constant
(c) its kinetic energy is constant
(d) it moves in a circular path.
No work is done by a force on an object if
(a) the force is always perpendicular to its velocity
(b) the force is always perpendicular to its acceleration
(c) the object is stationary but the point of application of the force moves on the object
(d) the object moves in such a way that the point of application of the force remains fixed.
A block of mass 5.0 kg slides down an incline of inclination 30° and length 10 m. Find the work done by the force of gravity.
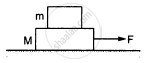
A block of mass m is kept over another block of mass M and the system rests on a horizontal surface (In the following figure). A constant horizontal force F acting on the lower block produces an acceleration \[\frac{F}{2 \left( m + M \right)}\] in the system, and the two blocks always move together. (a) Find the coefficient of kinetic friction between the bigger block and the horizontal surface. (b) Find the frictional force acting on the smaller block. (c) Find the work done by the force of friction on the smaller block by the bigger block during a displacement d of the system.
A box weighing 2000 N is to be slowly slid through 20 m on a straight track with friction coefficient 0⋅2 with the box. (a) Find the work done by the person pulling the box with a chain at an angle θ with the horizontal. (b) Find the work when the person has chosen a value of θ, which ensures him the minimum magnitude of the force.
A block of mass 2 kg kept at rest on an inclined plane of inclination 37° is pulled up the plane by applying a constant force of 20 N parallel to the incline. The force acts for one second. Find the kinetic energy of the block at the instant the force ceases to act. Take g = 10 m/s2.
A block of mass 2.0 kg is pushed down an inclined plane of inclination 37° with a force of 20 N acting parallel to the incline. It is found that the block moves on the incline with an acceleration of 10 m/s2. If the block started from rest, find the work done (a) by the applied force in the first second, (b) by the weight of the block in the first second and (c) by the frictional force acting on the block in the first second. Take g = 10 m/s2.
A 250 g block slides on a rough horizontal table. Find the work done by the frictional force in bringing the block to rest if it is initially moving at a speed of 40 cm/s. If the friction coefficient between the table and the block is 0⋅1, how far does the block move before coming to rest?
A block of mass 1 kg is placed at point A of a rough track shown in figure following. If slightly pushed towards right, it stops at point B of the track. Calculate the work done by the frictional force on the block during its transit from A to B.

A block of mass m is taken from A to B slowly under the action of a constant force R Work done by this force is ______.

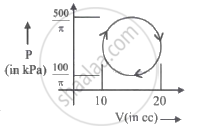
Work done by gas in cyclic process is ______ J.
Force acting on a particle is (2`hat"i"` + 3 `hat"j"`) N. Work done by this force is zero, when a particle is moved on the line 3y + kx = 5. Here value of k is ______.
