Advertisements
Advertisements
Question
A block of mass 5.0 kg slides down an incline of inclination 30° and length 10 m. Find the work done by the force of gravity.
Solution
\[\text{ Mass of the block, M = 5 kg }\]
\[\text{ Angle of inclination } , \theta = 30^\circ\]
Gravitational force acting on the block,
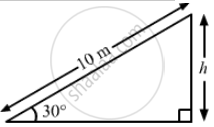
\[ = 10 \times \frac{1}{2} = 5 m\]
\[\therefore \text{ Work done by the force of gravity, w = mgh } \]
\[ = 5 \times 9 . 8 \times 5 = 245 J\]
APPEARS IN
RELATED QUESTIONS
A body constrained to move along the z-axis of a coordinate system is subject to a constant force F given by
`F = -hati+2hatj+3hatkN`
Where `hati,hatj,hatk` are unit vectors along the x-, y- and z-axis of the system respectively. What is the work done by this force in moving the body a distance of 4 m along the z-axis ?
A lawyer alleges in court that the police had forced his client to issue a statement of confession. What kind of force is this ?
A 60 kg man pushes a 40 kg man by a force of 60 N. The 40 kg man has pushed the other man with a force of
Mark the correct statements :
(a) The nuclear force between two protons is always greater than the electromagnetic force between them.
(b) The electromagnetic force between two protons is always greater than the gravitational force between them.
(c) The gravitational force between two protons may be greater than the nuclear force between them.
(d) Electromagnetic force between two protons may be greater than the nuclear force acting between them.
If all matters were made of electrically neutral particles such as neutrons,
(a) there would be no force of friction
(b) there would be no tension in the string
(c) it would not be possible to sit on a chair
(d) the earth could not move around the sun.
At what distance should two charges, each equal to 1 C, be placed so that the force between them equals your weight ?
Find the ratio of the magnitude of the electric force to the gravitational force acting between two protons.
The magnetic force on a charged particle is always perpendicular to its velocity. Can the magnetic force change the velocity of the particles? Speed of the particle?
The work done by the external forces on a system equals the change in
The work done by all the forces (external and internal) on a system equals the change in ______.
A block of mass m slides down a smooth vertical circular track. During the motion, the block is in
A constant force of 2⋅5 N accelerates a stationary particle of mass 15 g through a displacement of 2⋅5 m. Find the work done and the average power delivered.
A force \[F = \alpha + bx\] acts on a particle in the x-direction, where a and b are constants. Find the work done by this force during a displacement from x = 0 to x = d.
A block of mass 2 kg kept at rest on an inclined plane of inclination 37° is pulled up the plane by applying a constant force of 20 N parallel to the incline. The force acts for one second. Find the work done by the force of gravity in that one second if the work done by the applied force is 40 J.
A block of mass 2.0 kg is pushed down an inclined plane of inclination 37° with a force of 20 N acting parallel to the incline. It is found that the block moves on the incline with an acceleration of 10 m/s2. If the block started from rest, find the work done (a) by the applied force in the first second, (b) by the weight of the block in the first second and (c) by the frictional force acting on the block in the first second. Take g = 10 m/s2.
A uniform chain of length L and mass M overhangs a horizontal table with its two third part on the table. The friction coefficient between the table and the chain is μ . Find the work done by friction during the period the chain slips off the table.
A force F = 20 + 10y acts on a particle in y-direction where F is in newton and y in metre. Work done by this force to move the particle from y – 0 to y – 1 m is:
A body is moving unidirectionally under the influence of a source of constant power supplying energy. Which of the diagrams shown in figure correctly shows the displacement-time curve for its motion?
A body is displaced from (0, 0) to (1 m, 1 m) along the path x = y by a force F = (x2`hat"J"` + y`hat"i"`)N. The work done by this force will be:
