Advertisements
Advertisements
प्रश्न
A well with 10 m inside diameter is dug 8.4 m deep. Earth taken out of it is spread all around it to a width of 7.5 m to form an embankment. Find the height of the embankment.
उत्तर
Radius of well
`r = 10/2`
` = 5m`
Depth of well h = 8.4 m
Clearly,
Volume of earth dugout
`= pi(5)^2 xx 8.4`
`= pi xx 25 xx 8.4`
` =(22 xx 25 xx 8.4)/7 m^3`
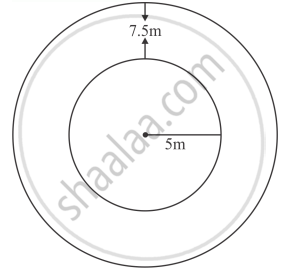
Let h' be the height of embankment
Clearly,
Embankment forms a cylindrical shell whose inner and outer radius are 5 m and 12.5 m respectively.
∴ Volume of the embankment
`= pi{(12.5)^2 - (5)^2} xx h``
` = pi xx 17.5 xx 7.5 xx h' m^3`
But, volume of earth dugout = volume of the embankment
`(22 xx 25 xx 8.4)/7 = 22/7 xx 17.5 xx 7.5 xx h`
` h = (25 xx 8.4)/(17.5 xx 7.5)`
`h` = 1.6 m`
APPEARS IN
संबंधित प्रश्न
A conical vessel, with base radius 5 cm and height 24 cm, is full of water. This water is emptied into a cylindrical vessel of base radius 10 cm. Find the height to which the water will rise in the cylindrical vessel. (use `pi=22/7`)
In a rectangular park of dimensions 50 m × 40 m, a rectangular pond is constructed so that the area of grass strip of uniform width surrounding the pond would be 1184 m2. Find the length and breadth of the pond ?
Find the volume of a cone if the radius of its base is 1.5 cm and its perpendicular height is 5 cm.
A spherical ball of iron has been melted and made into smaller balls. If the radius of each smaller ball is one-fourth of the radius of the original one, how many such balls can be made?
A toy is in the form of a cone mounted on a hemisphere of common base radius 7 cm. The total height of the toy is 31 cm. Find the total surface area of the toy.
From a solid cylinder whose height is 8 cm and radius 6 cm, a conical cavity of height 8 cm and base radius 6 cm is hollowed out. Find the volume of the remaining solid. Also, find the total surface area of the remaining solid.
Arrange the given objects according to their volume
The surface area of a sphere is 616 cm2. Its radius is ______.
______ surface area of room = area of 4 walls.
A boy is cycling such that the wheels of the cycle are making 140 revolutions per hour. If the diameter of the wheel is 60 cm, calculate the speed in km/h with which the boy is cycling.
