Advertisements
Advertisements
प्रश्न
A wire bent in the form of an equilateral triangle has an area of `121sqrt(3)"cm"^2`. If the same wire is bent into the form of a circle, find the area enclosed by the wire.
उत्तर
We know that, Area of an equilateral triangle(A) of side a is A = `sqrt(3)/(4)"a"^2`
Here, A = `121sqrt(3)`
⇒ `121sqrt(3) = sqrt(3)/(4)"a"^2`
⇒ 121 = `"a"^2/(4)`
⇒ 11 = `"a"/(2)`
⇒ a = 22
⇒ 3a = 66cm
The Circumference of a Circle with radius r = 2πr
Here,
66cm = 2πr
⇒ 66
⇒ r = 10.5cm
The Area of a Circle with radius r = πr2
The Area of a Circle with radius 10.5
= `(22)/(7)(10.5)^2`
= 346.5cm2.
APPEARS IN
संबंधित प्रश्न
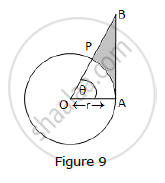
In Fig. 9, is shown a sector OAP of a circle with centre O, containing ∠θ. AB is perpendicular to the radius OQ and meets OP produced at B. Prove that the perimeter of shaded region is
`r[tantheta+sectheta+(pitheta)/180-1]`
An elastic belt is placed around the rim of a pulley of radius 5 cm. (Fig. 10) From one point C on the belt, the elastic belt is pulled directly away from the centre O of the pulley until it is at P, 10 cm from the point O. Find the length of the belt that is still in contact with the pulley. Also find the shaded area (use π = 3.14 and `sqrt3=1.73)`

The minute hand of a circular clock is 15 cm long. How far does the tip of the minute hand move in 1 hour. (Take π = 3.14)
Find the angle subtended at the centre of circle of radius ‘a’ cm by an arc of length
`(api)/4` 𝑐𝑚
A square ABCD is inscribed in a circle of radius r. Find the area of the square.
Find the area and perimeter of the circle with the following :
Radius= 2.8 cm
The area between the circumferences of two concentric circles is 2464 cm2. If the inner circle has circumference of 132 cm, calculate the radius of outer circle.
The diameter of a cycle wheel is `4(5)/(11)"cm"`. How many revolutions will it make in moving 6.3km?
Find the circumference of the circles whose radii are given below.
49 cm
A wheel of a car covers a distance of 3520 cm in 20 rotations. Find the radius of the wheel?
