Advertisements
Advertisements
प्रश्न
आफ़ताब अपनी पुत्री से कहता है, 'सात वर्ष पूर्व मैं तुमसे सात गुनी आयु का था। अब से 3 वर्ष बाद मैं तुमसे केवल तीन गुनी आयु का रह जाऊँगा। (क्या यह मनोरंजक है?)' इस स्थिति को बीजगणितीय एवं ग्राफीय रूपों में व्यक्त कीजिए।
उत्तर
माना आफ़ताब की वर्त्तमान आयु = x वर्ष
और उसकी पुत्री की वर्त्तमान आयु = y वर्ष
7 वर्ष पूर्व आफ़ताब की आयु = x - 7 वर्ष
और उसकी पुत्री की आयु = y - 7 वर्ष
स्थित - I
x - 7 = 7(y - 7)
x - 7 = 7y - 49
x - 7y = 7 - 49
x - 7y = -42 ..................(1)
3 वर्ष बाद आफ़ताब की आयु = x + 3 वर्ष
और उसकी पुत्री की आयु = y + 3 वर्ष
स्थित - II
x + 3 = 3(y + 3)
x + 3 = 3y + 9
x - 3y = 9 - 3
x - 3y = 6 ..............(2)
बीजगणितीय रूप में:
x - 7y = -42 .......(1)
x - 3y = 6 .................(2)
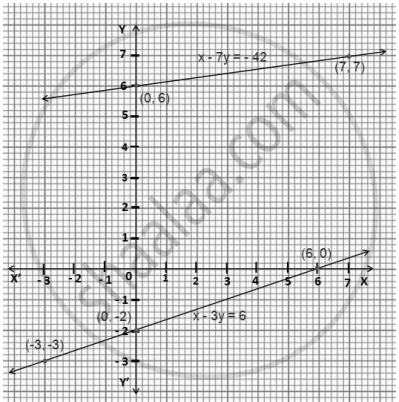
ग्राफीय रूप में प्रदर्शन:
x - 7y = -42
x = -42 + 7y
| x | -7 | 0 | 7 |
| y | 5 | 6 | 7 |
x - 3y = 6
x = 6 + 3y
| x | 0 | -3 | 6 |
| y | -2 | -3 | 0 |
APPEARS IN
संबंधित प्रश्न
अनुपातों `bb(a_1/a_2, b_1/b_2)` और `(c_1/c_2)` की तुलना कर ज्ञात कीजिए कि निम्न समीकरण युग्म द्वारा निरूपण रेखाएँ एक बिंदु पर प्रतिच्छेद करती हैं, समांतर हैं अथवा संपाती हैं:
5x - 4y + 8 = 0
7x + 6y - 9 = 0
निम्न रैखिक समीकरणों के युग्मों को हल कीजिए:
`x/a - y/b = 0`
ax + by = a2 + b2
निम्न रैखिक समीकरणों के युग्मों को हल कीजिए:
(a - b)x + (a + b)y = a2 - 2ab - b2
(a + b)(x + y) = a2 + b2
निम्न रैखिक समीकरणों के युग्मों को हल कीजिए:
152x - 378y = -74
-378x + 152y = -604
c का वह मान, जिसके लिए समीकरणों cx – y = 2 और 6x – 2y = 3 के युग्म के अपरिमित रूप से अनेक हल होंगे, है ______।
निम्नलिखित समीकरण-युग्मों (i) से (iv) में p और (v) में p तथा q के मान ज्ञात कीजिए :
3x – y – 5 = 0 और 6x – 2y – p = 0,
यदि इन समीकरणों द्वारा निरूपित रेखाएँ समांतर हैं।
निम्नलिखित समीकरण-युग्मों (i) से (iv) में p और (v) में p तथा q के मान ज्ञात कीजिए :
– x + py = 1 और px – y = 1,
यदि समीकरण-युग्म का कोई हल नहीं है।
निम्नलिखित समीकरण-युग्मों (i) से (iv) में p और (v) में p तथा q के मान ज्ञात कीजिए :
– 3x + 5y = 7 और 2px – 3y = 1
यदि इन समीकरणों द्वारा निरूपित रेखाएँ एक अद्वितीय बिंदु पर प्रतिच्छेद करती हैं।
निम्नलिखित समीकरण-युग्मों (i) से (iv) में p और (v) में p तथा q के मान ज्ञात कीजिए :
2x + 3y = 7 और 2px + py = 28 – qy,
यदि समीकरण-युग्म के अपरिमित रूप से अनेक हल हैं।
यदि 2x + y = 23 और 4x – y = 19 है, तो 5y – 2x और `y/x - 2` के मान ज्ञात कीजिए।
