Advertisements
Advertisements
प्रश्न
आकृती मध्ये M हा बाजू QR चा मध्यबिंदू आहे. ∠PRQ = 90° असेल तर सिद्ध करा, PQ2 = 4PM2 - 3PR2
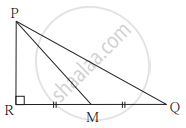
उत्तर
RM = `1/2`QR ....[M हा QR चा मध्यबिंदू आहे.]
∴ 2RM = QR ...(i)
ΔPQR मध्ये, ∠PRQ = 90° .....[पक्ष]
∴ PQ2 = PR2 + QR2 ...[पायथागोरसचे प्रमेय]
∴ PQ2 = PR2 + (2RM)2 ....[(i) वरून]
∴ PQ2 = PR2 + 4 RM2 ...(ii)
आता, ΔPRM मध्ये, ∠PRM = 90° .....[पक्ष]
∴ PM2 = PR2 + RM2 ...[पायथागोरसचे प्रमेय]
∴ RM2 = PM2 - PR2 .....(iii)
∴ PQ2 = PR2 + 4 (PM2 - PR2) ......[(ii) आणि (iii) वरून]
∴ PQ2 = PR2 + 4PM2 - 4PR2
∴ PQ2 = 4 PM2 - 3 PR2
APPEARS IN
संबंधित प्रश्न
रस्त्याच्या दुतर्फा असलेल्या इमारतीच्या भिंती एकमेकींना समांतर आहेत. 5.8 मी लांबीच्या शिडीचे एक टोक रस्त्यावर ठेवले असता तिचे वरचे टोक पहिल्या इमारतीच्या 4 मीटर उंच असलेल्या खिडकीपर्यंत टेकते. त्याच ठिकाणी शिडी ठेवून रस्त्याच्या दुसऱ्या बाजूस वळविल्यास तिचे वरचे टोक दुसऱ्या इमारतीच्या 4.2 मीटर उंच असलेल्या खिडकीपर्यंत येते, तर रस्त्याची रुंदी काढा.
बाजूंच्या लांबी a, b, c असलेल्या त्रिकोणामध्ये जर a2 + b2 = c2 असेल तर तो कोणत्या प्रकारचा त्रिकोण असेल?
काटकोन त्रिकोणामध्ये काटकोन करणाऱ्या बाजू 24 सेमी व 18 सेमी असतील तर त्याच्या कर्णाची लांबी ______ असेल.
आयताच्या बाजू 11 सेमी व 60 सेमी असतील, तर त्याच्या कर्णाची लांबी काढा.
एका काटकोन त्रिकोणामध्ये काटकोन करणाऱ्या बाजू 9 सेमी व 12 सेमी आहेत, तर त्या त्रिकोणाच्या कर्णाची लांबी काढा.
आयताचे क्षेत्रफळ 192 चौसेमी असून त्याची लांबी 16 सेमी आहे, तर आयताच्या कर्णाची लांबी काढा.
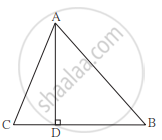
ΔABC मध्ये रेख AD ⊥ रेख BC आणि DB = 3CD, तर सिद्ध करा : 2AB2 = 2AC2 + BC2
एका काटकोन त्रिकोणामध्ये काटकोन करणाऱ्या बाजू 24 सेमी व 18 सेमी असतील, तर त्याच्या कर्णाची लांबी काढा.
काटकोन त्रिकोणात काटकोन करणाऱ्या बाजू 9 सेमी व 12 सेमी आहेत, तर त्या त्रिकोणाच्या कर्णाची लांबी माहीत करण्यासाठी कृती पूर्ण करा.
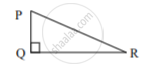
कृती: ∆PQR मध्ये, ∠PQR = 90°
पायथागोरसच्या प्रमेयानुसार,
PQ2 + `square` = PR2 .........…(i)
PR2 = 92 + 122
PR2 = `square + 144`
∴ PR2 = `square`
∴ PR = 15
त्रिकोणाचा कर्ण = `square`
सोबतच्या आकृतीत, ∆QPR मध्ये, ∠QPR = 90°, PM ⊥ QR, PM = 10, QM = 8 यावरून QR काढण्यासाठी खालील कृती पूर्ण करा.
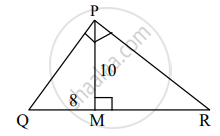
कृती:
∆PQR मध्ये, PM ⊥ QR
∠PMQ = 90°,
∆PMQ मध्ये, पायथागोरसच्या प्रमेयानुसार,
PM2 + `square` = PQ2 …(i)
∴ PQ2 = 102 + 82
∴ PQ2 = `square` + 64
PQ = `sqrt164`
∠PMR = 90°
यावरून, ∆QPR ~ ∆QMP ~ ∆PMR
∴ ∆QMP ~ ∆PMR
∴ `"PM"/"RM" = "QM"/"PM"`
∴ PM2 = RM × QM
∴ 102 = RM × 8
RM = `100/8 = square` आणि QR = QM + MR
QR = `square + 25/2 = 41/2`
