Advertisements
Advertisements
प्रश्न
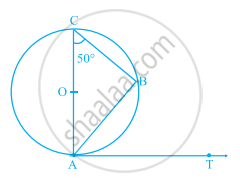
आकृति में, AB एक वृत्त की जीवा है तथा AOC वृत्त का व्यास इस प्रकार है कि ∠ACB = 50° है। यदि AT बिंदु A पर वृत्त की स्पर्श रेखा है, तो ∠BAT बराबर ______ है।
पर्याय
65°
60°
50°
40°
उत्तर
आकृति में, AB एक वृत्त की जीवा है तथा AOC वृत्त का व्यास इस प्रकार है कि ∠ACB = 50° है। यदि AT बिंदु A पर वृत्त की स्पर्श रेखा है, तो ∠BAT बराबर है 50° है।
स्पष्टीकरण:

आकृति में, AOC वृत्त का एक व्यास है।
हम जानते हैं कि, व्यास वृत्त पर 90° का कोण बनाता है।
तो, ∠ABC = 90°
ΔACB में,
∠A + ∠B + ∠C = 180° ...[चूँकि, त्रिभुज के सभी कोणों का योग 180° होता है।]
⇒ ∠A + 90° + 50° = 180°
⇒ ∠A + 140° = 180°
⇒ ∠A = 180° – 140° = 40°
∠A या ∠OAB = 40°
अब, AT बिंदु A पर वृत्त की स्पर्श रेखा है।
तो, OA, AT पर लंबवत है।
∴ ∠OAT = 90° ...[आकृति से]
⇒ ∠OAB + ∠BAT = 90°
∠OAB = 40° रखने पर, हमें प्राप्त होता है।
⇒ ∠BAT = 90° – 40° = 50°
अतः, ∠BAT का मान = 50° है।
APPEARS IN
संबंधित प्रश्न
एक वृत्त की _______ समांतर स्पर्श रेखाएँ हो सकती हैं।
वृत्त तथा उसकी स्पर्श रेखा के उभयनिष्ठ बिन्दु को _______ कहते हैं।
एक वृत्त खींचिए और दो एक दी गई रेखा के समांतर दो ऐसी रेखाएँ खींचिए कि उनमें से एक स्पर्श रेखा हो तथा दूसरी छेदक रेखा हो।
यदि दो संकेंद्रीय वृत्तों की त्रिज्याएँ 4 cm और 5 cm हैं, तो एक वृत्त की प्रत्येक उस जीवा की लंबाई, जो दूसरे वृत्त पर स्पर्श रेखा है, निम्नलिखित होगी ______।
किसी बिंदु P से, जो त्रिज्या 5 cm वाले एक वृत्त के केंद्र O से 13 cm की दूरी पर है, वृत्त पर दो स्पर्श रेखाएँ PQ और PR खींची गई हैं। तब चतुर्भुज PQOR का क्षेत्रफल ______ है।
AB = AC वाले एक समद्विबाहु त्रिभुज ABC के शीर्ष A पर त्रिभुज के परिवृत्त पर खींची गई स्पर्श रेखा भुजा BC के समांतर होती है।
यदि एक दिए हुए रेखाखंड PQ को कई वृत्त बिंदु A पर स्पर्श करते हैं, तो उनके केंद्र PQ के लंब समद्विभाजक पर स्थित होते है।
AB एक वृत्त का व्यास है और AC उसकी एक जीवा इस प्रकार है कि ∠BAC = 30° है। यदि C पर खींची गई स्पर्श रेखा बढ़ाई गई AB से D पर मिलती है, तो BC = BD होगा।
मान लीजिए कि s उस त्रिभुज ABC के अर्ध-परिमाप को व्यक्त करता है, जिसमें BC = a, CA = b और AB = c है। यदि एक वृत्त भुजाओं BC, CA और AB को क्रमश : D, E और F पर स्पर्श करता है, तो सिद्ध कीजिए कि BD = s – b है।
एक समकोण त्रिभुज ABC, जिसमें ∠B = 90° है, AB को व्यास मान कर एक वृत्त खींचा गया है, जो कर्ण AC को P पर प्रतिच्छेद करता है। सिद्ध कीजिए कि P पर वृत्त की स्पर्श रेखा BC को समद्विभाजित करती है।
