Advertisements
Advertisements
प्रश्न
AB = AC वाले एक समद्विबाहु त्रिभुज ABC के शीर्ष A पर त्रिभुज के परिवृत्त पर खींची गई स्पर्श रेखा भुजा BC के समांतर होती है।
पर्याय
सत्य
असत्य
उत्तर
यह कथन सत्य है।
स्पष्टीकरण:
माना EAF ∆ABC के परिवृत्त पर स्पर्श रेखा है।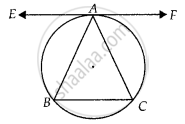
साबित करना : EAF ॥ BC
हमारे पास है, ∠EAB = ∠ACB ...(i) [स्पस्पर्श रेखा और जीवा के बीच का कोण जीवा द्वारा वैकल्पिक खंड में बनाए गए कोण के बराबर है।]
यहाँ AB = AC है।
⇒ ∠ABC = ∠ACB ...(ii)
समीकरण (i) और (ii) से हम पाते हैं,
∠EAB = ∠ABC
∵ एकांतर कोण बराबर होते हैं।
⇒ EAF ॥ BC
APPEARS IN
संबंधित प्रश्न
किसी वृत की स्पर्श रेखा उसे _____ बिन्दुओं पर प्रतिच्छेद करती है।
वृत्त को दो बिन्दुओं पर प्रतिच्छेद करने वाली रेखा को _____ कहते हैं।
एक वृत्त की _______ समांतर स्पर्श रेखाएँ हो सकती हैं।
5 सेमी त्रिज्या वाले एक वृत्त के बिन्दु P पर स्पर्श रेखा PQ केन्द्र O से जाने वाली एक रेखा से बिन्दु Q पर इस प्रकार मिलती है कि OQ = 12 सेमी। PQ की लम्बाई है।
किसी बिंदु P से, जो त्रिज्या 5 cm वाले एक वृत्त के केंद्र O से 13 cm की दूरी पर है, वृत्त पर दो स्पर्श रेखाएँ PQ और PR खींची गई हैं। तब चतुर्भुज PQOR का क्षेत्रफल ______ है।
यदि एक जीवा AB वृत्त के केंद्र पर 60° का कोण अंतरित करती (बनाती) है, तो A और B पर खींची गई स्पर्श रेखाओं के बीच का कोण भी 60° होगा।
किसी बाहरी बिंदु से एक वृत्त पर खींची गई स्पर्श रेखा की लंबाई सदैव उसकी त्रिज्या से बड़ी होती है।
यदि एक दिए हुए रेखाखंड PQ को कई वृत्त बिंदु A पर स्पर्श करते हैं, तो उनके केंद्र PQ के लंब समद्विभाजक पर स्थित होते है।
यदि एक षड्भुज ABCDEF एक वृत्त के परिगत है, तो सिद्ध कीजिए कि AB + CD + EF = BC + DE + FA है।
एक समकोण त्रिभुज ABC, जिसमें ∠B = 90° है, AB को व्यास मान कर एक वृत्त खींचा गया है, जो कर्ण AC को P पर प्रतिच्छेद करता है। सिद्ध कीजिए कि P पर वृत्त की स्पर्श रेखा BC को समद्विभाजित करती है।
