Advertisements
Advertisements
Question
AB = AC वाले एक समद्विबाहु त्रिभुज ABC के शीर्ष A पर त्रिभुज के परिवृत्त पर खींची गई स्पर्श रेखा भुजा BC के समांतर होती है।
Options
सत्य
असत्य
Solution
यह कथन सत्य है।
स्पष्टीकरण:
माना EAF ∆ABC के परिवृत्त पर स्पर्श रेखा है।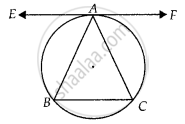
साबित करना : EAF ॥ BC
हमारे पास है, ∠EAB = ∠ACB ...(i) [स्पस्पर्श रेखा और जीवा के बीच का कोण जीवा द्वारा वैकल्पिक खंड में बनाए गए कोण के बराबर है।]
यहाँ AB = AC है।
⇒ ∠ABC = ∠ACB ...(ii)
समीकरण (i) और (ii) से हम पाते हैं,
∠EAB = ∠ABC
∵ एकांतर कोण बराबर होते हैं।
⇒ EAF ॥ BC
APPEARS IN
RELATED QUESTIONS
किसी वृत की स्पर्श रेखा उसे _____ बिन्दुओं पर प्रतिच्छेद करती है।
एक वृत्त की _______ समांतर स्पर्श रेखाएँ हो सकती हैं।
वृत्त तथा उसकी स्पर्श रेखा के उभयनिष्ठ बिन्दु को _______ कहते हैं।
5 सेमी त्रिज्या वाले एक वृत्त के बिन्दु P पर स्पर्श रेखा PQ केन्द्र O से जाने वाली एक रेखा से बिन्दु Q पर इस प्रकार मिलती है कि OQ = 12 सेमी। PQ की लम्बाई है।
एक वृत्त खींचिए और दो एक दी गई रेखा के समांतर दो ऐसी रेखाएँ खींचिए कि उनमें से एक स्पर्श रेखा हो तथा दूसरी छेदक रेखा हो।
यदि दो संकेंद्रीय वृत्तों की त्रिज्याएँ 4 cm और 5 cm हैं, तो एक वृत्त की प्रत्येक उस जीवा की लंबाई, जो दूसरे वृत्त पर स्पर्श रेखा है, निम्नलिखित होगी ______।
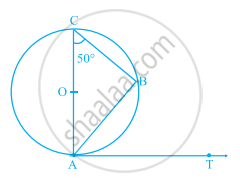
आकृति में, AB एक वृत्त की जीवा है तथा AOC वृत्त का व्यास इस प्रकार है कि ∠ACB = 50° है। यदि AT बिंदु A पर वृत्त की स्पर्श रेखा है, तो ∠BAT बराबर ______ है।
किसी बिंदु P से, जो त्रिज्या 5 cm वाले एक वृत्त के केंद्र O से 13 cm की दूरी पर है, वृत्त पर दो स्पर्श रेखाएँ PQ और PR खींची गई हैं। तब चतुर्भुज PQOR का क्षेत्रफल ______ है।
यदि किसी बिंदु P से त्रिज्या a और केंद्र O वाले वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण 60° है, तो OP = `asqrt(3)` होता है।
मान लीजिए कि s उस त्रिभुज ABC के अर्ध-परिमाप को व्यक्त करता है, जिसमें BC = a, CA = b और AB = c है। यदि एक वृत्त भुजाओं BC, CA और AB को क्रमश : D, E और F पर स्पर्श करता है, तो सिद्ध कीजिए कि BD = s – b है।
