Advertisements
Advertisements
Question
मान लीजिए कि s उस त्रिभुज ABC के अर्ध-परिमाप को व्यक्त करता है, जिसमें BC = a, CA = b और AB = c है। यदि एक वृत्त भुजाओं BC, CA और AB को क्रमश : D, E और F पर स्पर्श करता है, तो सिद्ध कीजिए कि BD = s – b है।
Solution
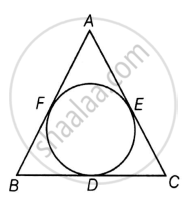
एक त्रिभुज ABC जिसमें BC = a, CA = b और AB = c है।
इसके अलावा, एक वृत्त खुदा हुआ है जो भुजाओं BC, CA और AB को क्रमशः D, E और F पर स्पर्श करता है और s त्रिभुज का अर्ध-परिधि है।
सिद्ध करना है: BD = s – b
सबूत:
हमारे पास है,
अर्ध-परिधि = s
परिमाप = 2s
2s = AB + BC + AC ...[1]
जैसा कि हम जानते हैं,
बाह्य बिंदु से वृत्त पर खींची गई स्पर्श रेखाएँ बराबर होती हैं।
तो हमारे पास
AF = AE ...[2] [बिंदु A से स्पर्शरेखा]
BF = BD ...[3] [बिंदु B से स्पर्शरेखा]
CD = CE ...[4] [बिंदु C से स्पर्शरेखा]
[2] [3] और [4] को जोड़ने पर,
AF + BF + CD = AE + BD + CE
AB + CD = AC + BD
दोनों पक्षों को BD जोड़ के,
AB + CD + BD = AC + BD + BD
AB + BC – AC = 2BD
AB + BC + AC – AC – AC = 2BD
2s – 2AC = 2BD ...[1 से]
2BD = 2s – 2b ...[चूंकि AC = b]
BD = s – b
अतः सिद्ध हुआ।
APPEARS IN
RELATED QUESTIONS
एक वृत्त में कितनी स्पर्श रेखाएँ हो सकती हैं?
एक वृत्त की _______ समांतर स्पर्श रेखाएँ हो सकती हैं।
वृत्त तथा उसकी स्पर्श रेखा के उभयनिष्ठ बिन्दु को _______ कहते हैं।
5 सेमी त्रिज्या वाले एक वृत्त के बिन्दु P पर स्पर्श रेखा PQ केन्द्र O से जाने वाली एक रेखा से बिन्दु Q पर इस प्रकार मिलती है कि OQ = 12 सेमी। PQ की लम्बाई है।
यदि दो संकेंद्रीय वृत्तों की त्रिज्याएँ 4 cm और 5 cm हैं, तो एक वृत्त की प्रत्येक उस जीवा की लंबाई, जो दूसरे वृत्त पर स्पर्श रेखा है, निम्नलिखित होगी ______।
किसी बिंदु P से, जो त्रिज्या 5 cm वाले एक वृत्त के केंद्र O से 13 cm की दूरी पर है, वृत्त पर दो स्पर्श रेखाएँ PQ और PR खींची गई हैं। तब चतुर्भुज PQOR का क्षेत्रफल ______ है।
AB = AC वाले एक समद्विबाहु त्रिभुज ABC के शीर्ष A पर त्रिभुज के परिवृत्त पर खींची गई स्पर्श रेखा भुजा BC के समांतर होती है।
यदि एक दिए हुए रेखाखंड PQ को कई वृत्त बिंदु A पर स्पर्श करते हैं, तो उनके केंद्र PQ के लंब समद्विभाजक पर स्थित होते है।
AB एक वृत्त का व्यास है और AC उसकी एक जीवा इस प्रकार है कि ∠BAC = 30° है। यदि C पर खींची गई स्पर्श रेखा बढ़ाई गई AB से D पर मिलती है, तो BC = BD होगा।
यदि एक षड्भुज ABCDEF एक वृत्त के परिगत है, तो सिद्ध कीजिए कि AB + CD + EF = BC + DE + FA है।
