Advertisements
Advertisements
प्रश्न
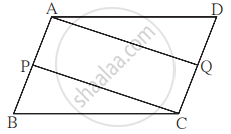
आकृति में, `square` ABCD समांतर चतुर्भुज है। बिंदु P तथा बिंदु Q क्रमशः भुजा AB तथा भुजा DC के मध्यबिंदु हैं तो सिद्ध कीजिए कि `square` APCQ समांतर चतुर्भुज है।
उत्तर
दत्त: `square` ABCD समांतर चतुर्भुज है।
भुजा AB तथा भुजा DC के मध्यबिंदु क्रमशः P तथा Q है।
साध्य: `square` APCQ समांतर चतुर्भुज है।
उपपत्ति:
रेख AB ≅ रेख DC ....( समांतर चतुर्भुज की सम्मुख भुजाएँ समांतर है।)
∴ रेख AP ≅ रेख CQ .....(A-P-B, C-Q-D) ....(i)
AB = CD ....(समांतर चतुर्भुज की सम्मुख भुजाएँ)
∴ `1/2` AB = `1/2` CD .....( दोनों पक्षों में `1/2` का गुणन करने पर)
परंतु , `1/2` AB = AP ....( बिंदु P, रेखा AB का मध्यबिंदु है।) ...(ii)
और `1/2` CD =CQ ....(बिंदु Q, रेखा CD का मध्यबिंदु है।) ....(iii)
∴ AP = CQ ....[(i), (ii) और (iii) से]
रेख AP || रेख CQ ....[(i) से]
रेख AP ≅ रेख CQ ....[(iv) से]
समांतर चतुर्भुज सम्मुख भुजाओं की एक जोड़ी समांतर और सर्वांगसम होती है।
इसी प्रकार हम सिद्ध कर सकते हैं कि `square` APCQ समांतर चतुर्भुज हैं ।
APPEARS IN
संबंधित प्रश्न
E एक ∆ABC की माध्यिका AD का मध्य-बिंदु है तथा BE को AC को F पर मिलने के लिए बढ़ाया गया है। दर्शाइए कि AF = `1/3` AC है।
दर्शाइए कि किसी वर्ग की क्रमागत भुजाओं के मध्य-बिंदुओं को मिलाने पर बना चतुर्भुज भी एक वर्ग होता है।
P एक समांतर चतुर्भुज ABCD की भुजा CD का मध्य-बिंदु है। C से होकर PA के समांतर खींची गई रेखा AB को Q पर तथा बढ़ाई हुई DA को R पर मिलती है। सिद्ध कीजिए कि DA = AR और CQ = QR है।
