Advertisements
Advertisements
प्रश्न
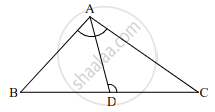
आकृतीमध्ये त्रिकोण ABC मध्ये बाजू BC वर D हा बिंदू असा आहे, की ∠BAC = ∠ADC. तर सिद्ध करा, की CA2 = CB × CD.
उत्तर
∆BAC व ∆ADC मध्ये,
∠BAC ≅ ∠ADC ...............[पक्ष]
∠BCA ≅ ∠ACD ..............[सामाईक कोन]
∴ ∆BAC ∼ ∆ADC ............[समरूपतेची कोको कसोटी]
∴ `"CA"/"CD" = "CB"/"CA"` ..........[समरूप त्रिकोणांच्या संगत बाजू]
∴ CA × CA = CB × CD
∴ CA2 = CB × CD
APPEARS IN
संबंधित प्रश्न
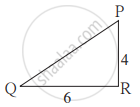
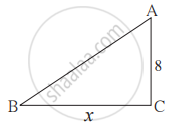
आकृती मध्ये दाखवल्याप्रमाणे 8 मीटर व 4 मीटर उंचीचे दोन खांब सपाट जमिनीवर उभे आहेत. सूर्यप्रकाशाने लहान खांबाची सावली 6 मीटर पडते, तर त्याच वेळी मोठ्या खांबाची सावली किती लांबीची असेल?
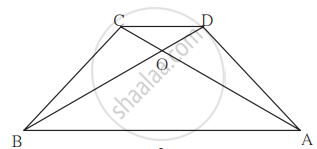
समलंब चौकोन ABCD मध्ये, बाजू AB || बाजू DC कर्ण AC व कर्ण BD हे परस्परांना O बिंदूत छेदतात. AB = 20, DC = 6, OB = 15 तर OD काढा.
खालीलपैकी कोणती कसोटी समरूपतेची नाही?
आकृतीमधील त्रिकोण समरूप आहेत का? असतील तर कोणत्या कसोटीनुसार?
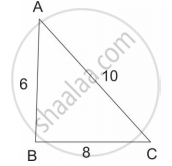
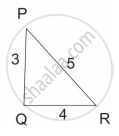
आकृतीचे निरीक्षण करा. ∆ABC व ∆PQR कोणत्या कसोटीनुसार समरूप आहेत? कसोटीचे नाव लिहा.

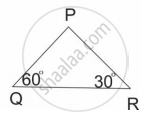
शेजारील आकृतीमध्ये, BP लंब AC, CQ लंब AB, A-P-C आणि A-Q-B, तर ∆APB व ∆AQC समरूप दाखवा.
∆APB व ∆AQC मध्ये,
∠APB = `square^circ` ......(i)
∠AQC = `square^circ` ......(ii)
∠APB ≅ ∠AQC …[(i) व (ii) वरून]
∠PAB ≅ ∠QAC .............` square`
∆APB ~ ∆AQC .............` square`
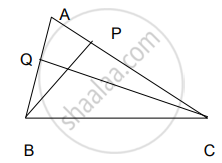
आकृतीचे निरीक्षण करून कृती पूर्ण करा.
आकृतीमध्ये, ∠B = 75°, ∠D = 75°
∠B ≅ ______ .............[प्रत्येकी 75°]
∠C ≅ ∠C ..................[______]
∆ABC ~ ∆[______] ..............[______ समरूपता कसोटीनुसार]

चौकोन ABCD मध्ये बाजू AD || BC, कर्ण AC आणि BD परस्परांना P बिंदूत छेदतात, तर सिद्ध करा, की `"AP"/"PD" = "PC"/"BP".`
जर ΔABC ∼ ΔDEF आणि ∠A = 48°, तर ∠D = ______.
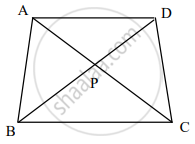
समलंब चौकोन ABCD मध्ये बाजू AB || बाजू CD चौकोनाचे कर्ण हे एकमेकांना बिंदू P मध्ये छेदतात.
त्यावरून खालील प्रश्नांची उत्तरे लिहा:
- वरील दिलेल्या माहितीवरून आकृती काढा.
- व्युत्क्रम कोन व विरुद्ध कोनांची प्रत्येकी एक जोडी लिहा.
- समरूप त्रिकोणांची नावे समरूपतेच्या कसोटीसह लिहा.
