Advertisements
Advertisements
प्रश्न
आयुष अपने घर से कार्यालय की ओर चलना प्रारंभ करता है। सीधे कार्यालय जाने के स्थान पर, पहले वह एक बैंक में जाता है, वहाँ से वह अपनी पुत्री के स्कूल और फिर कार्यालय पहुँचता है। यदि घर (2, 4) पर स्थित है, बैंक (5, 8) पर स्थित है, स्कूल (13, 14) पर स्थित है और कार्यालय (13, 26) पर स्थित है, तथा निर्देशांक किलोमीटर में हैं, तो आयुष ने कार्यालय पहुँचने के लिए कितनी अतिरिक्त दूरी चली है? (कल्पना कीजिए कि सभी तय की गई दूरियाँ सरल रेखाओं में हैं।)
उत्तर
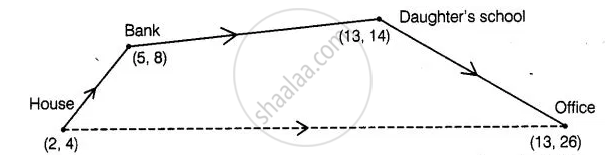
दी गई शर्त के अनुसार, हमने एक आकृति बनाई है जिसमें हर स्थान को उसके निर्देशांक और दिशा के साथ भी दर्शाया गया है।
हम जानते हैं कि,
दो बिंदुओं के बीच की दूरी
अब, घर और बैंक के बीच की दूरी =
=
=
=
= 5
बैंक और बेटी के स्कूल के बीच की दूरी =
=
=
=
= 10
बेटी के स्कूल और कार्यालय के बीच की दूरी =
=
= 12
कुल दूरी (घर + बैंक + स्कूल + कार्यालय) तय की = 5 + 10 + 2 = 27 units
घर से कार्यालय की दूरी =
=
=
=
= 24.59
= 24.6 किलोमीटर
इसलिए, आयुष द्वारा अपने कार्यालय तक पहुँचने में तय की गई अतिरिक्त दूरी = 27 – 24.6 = 2.4 किलोमीटर
इसलिए, आयुष द्वारा तय की गई आवश्यक अतिरिक्त दूरी 2.4 किमी है।
APPEARS IN
संबंधित प्रश्न
बिंदु P(– 4, 2), बिंदुओं A(– 4, 6) और B(– 4, – 6) को मिलाने वाले रेखाखंड पर स्थित हैं।
यदि (– 4, 3) और (4, 3) एक समबाहु त्रिभुज के दो शीर्ष हैं, तो इस त्रिभुज के तीसरे शीर्ष के निर्देशांक ज्ञात कीजिए, जब कि दिया है कि मूलबिंदु त्रिभुज के अभ्यंतर में स्थित है।
A(x1, y1), B(x2, y2) और C(x3, y3) एक ΔABC के शीर्ष हैं। AD पर स्थित उस बिंदु P के निर्देशांक ज्ञात कीजिए, जिससे AP : PD = 2 : 1 हो।
A(x1, y1), B(x2, y2) और C(x3, y3) एक ΔABC के शीर्ष हैं। माध्यिकाओं BE और CF पर स्थित क्रमश : ऐसे बिंदुओं Q और R के निर्देशांक ज्ञात कीजिए कि BQ : QE = 2 : 1 और CR : RF = 2 : 1 हो।
A(x1, y1), B(x2, y2) और C(x3, y3) एक ΔABC के शीर्ष हैं। ΔABC के केंद्रक के क्या निर्देशांक हैं?
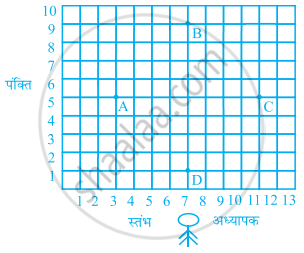
किसी स्कूल के विद्यार्थी ड्रिल अभ्यास के लिए, अपने खेल के मैदान में पंक्तियों और स्तंभों में खड़े हैं। A, B, C और D किन्ही चार विद्यार्थियों के स्थान हैं, जैसा आकृति में दर्शाया गया है। क्या यह संभव है कि इस ड्रिल में जसपाल को ऐसे स्थान पर खड़ा कर दिया जाए कि वह A, B, C और D से समदूरस्थ हो? यदि ऐसा है तो उसकी स्थिति कहाँ होगी?
बिंदु (-3, 5) स्थित है : ______
किसी बिंदु का भुज धनात्मक होता है :
बिंदु (3, 0) प्रथम चतुर्थांश में स्थित है।
बिंदु (-4, -3) किस चतुर्थांश में होगा?
