Advertisements
Advertisements
प्रश्न
आयुष अपने घर से कार्यालय की ओर चलना प्रारंभ करता है। सीधे कार्यालय जाने के स्थान पर, पहले वह एक बैंक में जाता है, वहाँ से वह अपनी पुत्री के स्कूल और फिर कार्यालय पहुँचता है। यदि घर (2, 4) पर स्थित है, बैंक (5, 8) पर स्थित है, स्कूल (13, 14) पर स्थित है और कार्यालय (13, 26) पर स्थित है, तथा निर्देशांक किलोमीटर में हैं, तो आयुष ने कार्यालय पहुँचने के लिए कितनी अतिरिक्त दूरी चली है? (कल्पना कीजिए कि सभी तय की गई दूरियाँ सरल रेखाओं में हैं।)
उत्तर
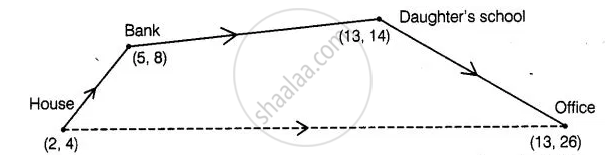
दी गई शर्त के अनुसार, हमने एक आकृति बनाई है जिसमें हर स्थान को उसके निर्देशांक और दिशा के साथ भी दर्शाया गया है।
हम जानते हैं कि,
दो बिंदुओं के बीच की दूरी `(x_1, "y"_1)` और `(x_2, "y"_2)`,
`"d" = sqrt((x_2 - x_1)^2 + ("y"_2 - "y"_1)^2`
अब, घर और बैंक के बीच की दूरी = `sqrt((5 - 2)^2 + (8 - 4)^2`
= `sqrt((3)^2 + (4)^2`
= `sqrt(9 + 16)`
= `sqrt(25)`
= 5
बैंक और बेटी के स्कूल के बीच की दूरी = `sqrt((13 - 5)^2 + (14 - 8)^2`
= `sqrt((8)^2 + (6)^2`
= `sqrt(64 + 36)`
= `sqrt(100)`
= 10
बेटी के स्कूल और कार्यालय के बीच की दूरी = `sqrt((13 - 13)^2 + (26 - 14)^2`
= `sqrt(0 + (12)^2`
= 12
कुल दूरी (घर + बैंक + स्कूल + कार्यालय) तय की = 5 + 10 + 2 = 27 units
घर से कार्यालय की दूरी = `sqrt((13 - 2)^2 + (26 + 4)^2`
= `sqrt((11)^2 + (22)^2`
= `sqrt(121 + 484)`
= `sqrt(605)`
= 24.59
= 24.6 किलोमीटर
इसलिए, आयुष द्वारा अपने कार्यालय तक पहुँचने में तय की गई अतिरिक्त दूरी = 27 – 24.6 = 2.4 किलोमीटर
इसलिए, आयुष द्वारा तय की गई आवश्यक अतिरिक्त दूरी 2.4 किमी है।
APPEARS IN
संबंधित प्रश्न
एक अन्य व्यक्ति को आप अपने अध्ययन मेज पर रखे टेबल लैंप की स्थिति किस तरह बताएँगे?
बिंदु P(2, 3) की x-अक्ष से दूरी ______ है।
बिंदु P(5, –3), बिंदुओं A(7, –2) और B(1, –5) को मिलाने वाले रेखाखंड को समत्रिभाजित करने वाले दो बिंदुओं में से एक बिंदु है।
बिंदु (-3, 5) स्थित है : ______
वह बिंदु जिसके दोनों निर्देशांक ऋणात्मक हैं स्थित होगा :
बिंदु (1, – 1), (2, – 2), (4, – 5), (– 3, – 4) ______ ।
निम्नलिखित बिंदुओं को आलेखित कीजिए तथा जाँच कीजिए कि ये संरेख हैं या नहीं :
(1, 1), (2, – 3), (– 1, – 2)
निम्नलिखित बिंदुओं को आलेखित कीजिए तथा जाँच कीजिए कि ये संरेख हैं या नहीं :
(0, 0), (2, 2), (5, 5)
उस बिंदु के निर्देशांक ज्ञात कीजिए, जो जिसकी कोटि – 4 है और जो y-अक्ष पर स्थित है।
P(-1, 1), Q(3, -4), R(1, -1), S(-2, -3), T(-4, 4) में से चतुर्थ चतुर्थांश के बिंदु कौन-से हैं?
