Advertisements
Advertisements
प्रश्न
ABCD एक समचतुर्भुज इस प्रकार है कि AB का लंब समद्विभाजक D से होकर जाता है। इस समचतुर्भुज के कोण ज्ञात कीजिए।
संकेत : BD को मिलाइए। तब ΔABD एक समबाहु त्रिभुज है।
उत्तर
मान लीजिए ABCD एक समचतुर्भुज है, जहाँ DE, AB का लंब समद्विभाजक है।
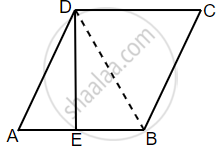
निर्माण: BD को मिलाएं।
अब, त्रिभुज AED और त्रिभुज BED में:
AE = EB
ED = ED ...[सामान्य पक्ष]
∠AED = ∠DEB = 90°
अब, SAS नियम का उपयोग करते हुए,
ΔAED ≅ BED
AD = DB = AB ...[ABCD एक समचतुर्भुज है। तो, AD = AB]
अत:, त्रिभुज ADB एक समबाहु त्रिभुज है।
तो, ∠DAB = ∠DBA = ∠ADB = 60°
∴ ∠DCB = 60° ...[समचतुर्भुज के सम्मुख कोण बराबर होते हैं।]
अब, ∠DAB + ∠ABC = 180° ...[एक समचतुर्भुज के आसन्न कोण संपूरक होते हैं।]
⇒ 60° + ∠ABD + ∠DBC = 180°
⇒ 60° + 60° + ∠DBC = 180°
⇒ ∠DBC = 60°
∴ ∠ABC = ∠ABD + ∠DBC = 60° + 60° = 120°
∴ ∠ADC = 120° ...[एक समचतुर्भुज के सम्मुख कोण बराबर होते हैं।]
अतः, समचतुर्भुज के कोण 60°, 120°, 60°, 120° हैं।
APPEARS IN
संबंधित प्रश्न
बताइए कैसे वर्ग एक समचतुर्भुज है।
यदि किसी समांतर चतुर्भुज की आसनन भुजाएँ बराबर हों, तो वह समांतर चतुर्भुज होता है एक ______।
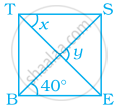
दी हुई आकृति में, BEST एक समचतुर्भुज है। तब, y – x का मान है –
एक चतुर्भुज, जो समांतर चतुर्भुज नहीं है परंतु जिसमें सम्मुख कोणों का ठीक एक युग्म बराबर है, ______ होता है।
सभी समचतुर्भुज वर्ग होते हैं।
किसी घर के फर्श पर एक रंगोली बनायी गयी है। इसमें, ABCD और PQRS दोनों समचतुर्भुजों के आकर के हैं। समचतुर्भुज ABCD की प्रत्येक भुजा पर खींचे गये अर्धवृत्त की त्रिज्या ज्ञात कीजिए।
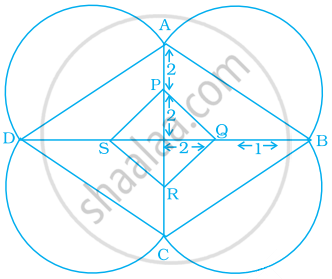
एक समचतुर्भुज CLUE की रचना कीजिए, जिसमें CL = 7.5 cm और LE = 6 cm है।
समांतर `square` ABCD के विकर्ण एक-दूसरे को बिंदु O पर प्रतिच्छेदित करते हैं। यदि AO = 5, BO = 12 तथा AB = 13 तो सिद्ध कीजिए कि `square` ABCD समचतुर्भुज है।
किसी समचतुर्भुज के विकर्णों की लंबाई क्रमशः 20 सेमी, 21 सेमी है तो उस चतुर्भुज की भुजा तथा परिमिति ज्ञात कीजिए।
समचर्तुभुज PQRS के विकर्ण PR तथा विकर्ण QS की लंबाई क्रमशः 20 सेमी तथा 48 सेमी है तो समचर्तुभुज की भुजा PQ की लंबाई ज्ञात कीजिए।
