Advertisements
Advertisements
प्रश्न
अक्षों के बीच रेखाखंड को बिंदु R(h, k), 1 : 2 के अनुपात में विभक्त करता है। रेखा का समीकरण ज्ञात कीजिए।
उत्तर
मान लीजिए AB अक्षों के बीच का रेखाखंड इस प्रकार है कि बिंदु R (h,k) AB को 1 : 2 के अनुपात में विभक्त करता है।
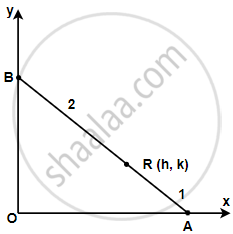
माना A और B के संबंधित निर्देशांक (x, 0) और (0, y) हैं।
चूँकि बिंदु R (h, k) खंड सूत्र के अनुसार AB को 1 : 2 के अनुपात में विभक्त करता है,
(h, k) = `(1 xx 0 + 2 xx x)/(1 + 2), (1 xx y + 2 xx 0)/(1 + 2)`
= (h, k) = `((2x)/3, y/3)`
= `h = (2x)/3 और k = y/3`
= x = `(3h)/2 और y = 3k`
इसलिए, A और B के संबंधित निर्देशांक `((3h)/2,0)` और (0, 3k) हैं।
अब, बिंदु `((3h)/2,0)` और (0, 3k) से जाने वाली रेखा AB का समीकरण है
(y - 0) = `(3k - 0)/(0 - (3h)/2) (x - (3h)/2)`
y = `(2k)/h (x - (3h)/2)`
hy = `-(2k)/h (x - (3h)/2)`
hy = -2kx + 3hk
अर्थात, 2kx + hy = 3hk
इस प्रकार, रेखा का आवश्यक समीकरण 2kx + hy = 3hk है।
APPEARS IN
संबंधित प्रश्न
निम्नलिखित रेखा का समीकरण ज्ञात कीजिए जो दिये गये प्रतिबंध को संतुष्ट करता है:
x-अक्ष और y-अक्ष के समीकरण लिखिए।
निम्नलिखित रेखा का समीकरण ज्ञात कीजिए जो दिये गये प्रतिबंध को संतुष्ट करता है:
बिंदु (0, 0) से जाने वाली और ढाल m वाली।
निम्नलिखित रेखा का समीकरण ज्ञात कीजिए जो दिये गये प्रतिबंध को संतुष्ट करता है:
बिंदुओं (−1, 1) और (2, –4) से जाते हुए।
उस रेखा का समीकरण ज्ञात कीजिए जिसकी मूल बिंदु से लांबिक दूरी 5 इकाई और लंब, धन x-अक्ष से 30° का कोण बनाती है।
रेखा का समीकरण ज्ञात कीजिए जो दिये गये प्रतिबंध को संतुष्ट करता है:
∆PQR के शीर्ष P(2, 1), Q(−2, 3) और R(4, 5) हैं। शीर्ष R से जाने वाली माध्यिका का समीकरण ज्ञात कीजिए।
(−3, 5) से होकर जाने वाली और बिंदु (2, 5) और (−3, 6) से जाने वाली रेखा पर लंब रेखा का समीकरण ज्ञात कीजिए।
एक रेखा (1, 0) तथा (2, 3) बिंदुओं को मिलाने वाली रेखा खंड पर लंब है तथा उसको 1 : n के अनुपात में विभाजित करती है। रेखा का समीकरण ज्ञात कीजिए।
एक रेखा का समीकरण ज्ञात कीजिए जो निर्देशांकों से समान अंत: खंड काटती है और बिंदु (2, 3) से जाती है।
बिंदु (2, 2) से जाने वाली रेखा का समीकरण ज्ञात कीजिए जिसके द्वारा अक्षों से कटे अंतः खंडों का योग 9 है।
ताँबे की छड़ की लंबाई L (सेमी में) सेल्सियस ताप C का रैखिक फलन है। एक प्रयोग में यदि L = 124.942 जब C = 20 और L = 125.134 जब C = 110 हो, तो L को C के पदों में व्यक्त कीजिए।
अक्षों के बीच रेखाखंड का मध्य बिंदु P(a, b) है। दिखाइए कि रेखा का समीकरण `"x"/"a" + "y"/"b" = 2` हैं।
निम्नलिखित समीकरण को लंब रूप में रूपांतरित कीजिए। उनकी मूल बिंदु से लांबिक दूरियाँ और लंब तथा धन x-अक्ष के बीच का कोण ज्ञात कीजिए:
x – y = 4
θ और p के मान ज्ञात कीजिए यदि समीकरण x cos θ + y sin θ = p रेखा `sqrt3`x + y + 2 = 0 का लंब रूप है।
रेखाओं y – x = 0, x + y = 0, और x – k = 0 से बने त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
रेखाओं 4x + 7y – 3 = 0 और 2x – 3y + 1 = 0 के प्रतिच्छेद बिंदु से जाने वाली रेखा का समीकरण ज्ञात कीजिए जो अक्षों से समान अंतः खंड बनाती हैं।
किसी बिंदु के लिए रेखा को दर्पण मानते हुए बिंदु (3, 8) का रेखा x + 3y = 7 में प्रतिबिंब ज्ञात कीजिए।
यदि रेखाएँ y = 3x + 1 और 2y = x + 3, रेखा y = mx + 4, पर समान रूप से आनत हों तो m का मान ज्ञात कीजिए।
निम्नलिखित समीकरण को ढाल-अंतः खंड रूप में रूपांतरित कीजिए और उनके ढाल तथा y-अंतः खंड ज्ञात कीजिए:
x + 7y = 0
निम्नलिखित समीकरण को अंतः खंड रूप में रूपांतरित कीजिए और अक्षों पर इनके द्वारा काटे गए अंतः खंड ज्ञात कीजिए:
4x – 3y = 6
निम्नलिखित समीकरण को लंब रूप में रूपांतरित कीजिए। उनकी मूल बिंदु से लांबिक दूरियाँ और लंब तथा धन x-अक्ष के बीच का कोण ज्ञात कीजिए:
`x - sqrt3y + 8 = 0`
निम्नलिखित समीकरण को लंब रूप में रूपांतरित कीजिए। उनकी मूल बिंदु से लांबिक दूरियाँ और लंब तथा धन x-अक्ष के बीच का कोण ज्ञात कीजिए:
y – 2 = 0
