Advertisements
Advertisements
प्रश्न
(a) An emf e = e0 sin ωt applied to a series L - C - R circuit derives a current I = I0sinωt in the circuit. Deduce the expression for the average power dissipated in the circuit.
(b) For circuits used for transporting electric power, a low power factor implies large power loss in transmission. Explain.
उत्तर
Instantaneous power,
P = ei = (e0 sin ωt) [i0 sin (ωt ± Φ)]
= e0i0 sin ωt (sin ωt cos Φ ± cos ωt sin Φ)
= e0i0 cos Φ sin2 ωt ± e0i0 sin Φ sin ωt cos ωt
Average power over one cycle,
`"P"_"av" = "work done in one cycle"/"time for one cycle"`
`= (int_0^"T" "P dt")/"T"`
`= (int_0^"T" ["e"_0"i"_0 cos phi sin^2 omega"t" +- "e"_0"i"_0 sin phi sin omega "t"]"dt")/"T"`
`= ("e"_0"i"_0)/"T" [cos phi int_0^"T" sin^2 omega "t dt" +- sin phi int_0^"T" sin omega "t" cos omega "t" "dt"]`
Now, `int_0^"T" sin^2 omega "t dt" = int_0^"T" ((1 - cos 2 omega "t")/2)`dt
`= int_0^"T" 1/2 "dt" - int_0^"T" (cos 2 omega "t")/2 "dt" = "T"/2 - 1/2 ((sin 2 omega "t")/(2omega))_0^"T"`
`= "T"/2 - 1/(4omega)(sin 2omega"T" - sin 0)`
`= "T"/2 - 1/(4omega) [sin 2((2pi)/"T")"T" - 0]`
`= "T"/2 - 1/(4omega) [0 - 0] = "T"/2`
Also,
`int_0^"T" sin omega"t" cos omega"t" "dt" = 1/2 int_0^"T" sin 2 omega"t" "dt" = 1/2 [(- cos 2 omega"t")/(2omega)]_0^"T"`
`= - 1/(4omega) [cos 2((2pi)/"T")"T" - cos 0] = - 1/(4omega)[1 - 1] = 0`
Hence, `"P"_"av" = ("e"_0"i"_0)/"T" cos phi xx "T"/2 = ("e"_0"i"_0)/2 cos phi`
`= "e"_0/sqrt2 * "i"_0/sqrt2 cos phi`
`= "e"_"rms""i"_"rms" cos phi = "e"_"rms""i"_"rms" ("R"/"Z")`, where the impedance Z = `sqrt("R"^2 +("X"_"L" - "X"_"C")^2)`
(b) `"P"_"av" = "e"_"rms""i"_"rms" cos phi`
The cos Φ factor is also known as the power factor. A low power factor in a circuit used to transport electric power means that the power available on transportation is much less than `"e"_"rms""i"_"rms"`. It denotes a significant loss of power during transport.
APPEARS IN
संबंधित प्रश्न
Obtain an expression for average power dissipated in a purely resistive A.C. circult.
A resistor of 500 Ω and an inductance of 0.5 H are in series with an AC source which is given by V = `100 sqrt2` sin (1000 t). The power factor of the combination is ______.
Answer in brief.
What is wattles current?
An AC source generating a voltage e = e0sinωt is connected to a capacitor of capacitance C. Find the expression for the current i flowing through it. Plot a graph of e and i versus ωt.
An AC circuit consists of only an inductor of inductance 2 H. If the current is represented by a sine wave of amplitude 0.25 A and frequency 60 Hz, calculate the effective potential difference across the inductor. (π = 3.142)
A 100 μF capacitor is charged with a 50 V source supply. Then source supply is removed and the capacitor is connected across an inductance, as a result of which 5A current flows through the inductance. Calculate the value of the inductance.
Give any one definition of power factor.
L-C-R series circuit contains a resistance of 10 Ω and self-inductance 0.4 H connected in series with variable capacitor across 60 V and 50 Hz supply. The value of capacity at resonance will be π2 = 10.
An alternating e.m.f. of 0.2 V is applied across an LCR series circuit having R = 4 `Omega`, C = 80 µF and L = 200 mH. At resonance the voltage drop across the inductor is ____________.
In series 'LR' circuit and in series 'RC' circuit, same current is flowing. If the frequency of e.m.f. of a.c. is increased for both the circuits, the impedance will ____________.
In series LCR circuit, resistance is 18 `Omega` and impedance is 33 `Omega`. An r.m.s. voltage of 220 V is applied across the circuit. The true power consumed in a.c. circuit is ____________.
In LCR series circuit, an alternating e.m.f. 'e' and current 'i' are given by the equations e = 100 sin (100 t) volt,
`"i" = 100 "sin" (100"t" + pi/3)"mA"`.
The average power dissipated in the circuit will be ____________.
An e.m.f. E = E0 sin `omega`t is applied to a circuit containing 'L' and 'R' in series. If XL = R, then the power dissipated in the circuit is ____________.
The voltage gain of a CE amplifier is 50. A sinusoidal ac of amplitude 10 mV is applied as a signal. The output of the amplifier will be ______.
In a series LR circuit XL = R and power factor of the circuit is P1. When capacitor with capacitance C such that XL= XC is put in series, the power factor becomes P2. The ratio `"P"_1/"P"_2` is ______.
Two unknown resistances are connected in two gaps of a meter-bridge. The null point is obtained at 40 cm from left end. A 30 Ω resistance is connected in series with the smaller of the two resistances, the null point shifts by 20 cm to the right end. The value of smaller resistance Ω is ______.
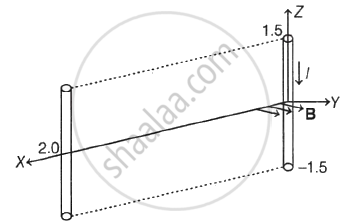
A conductor lies along the Z-axis at −1.5 ≤ Z ≤ 1.5 m and carries a fixed current of 10.0 A in −az direction as (see figure). For a field B = 3.0 × 10−4`"e"^(−0.2"x")`ay T, find the power required to move the conductor at constant speed to x = 2.0 m, y = 0 in 5 × 10−3 s. Assume parallel motion along the x-axis.
What is the average value of alternating current over a complete cycle?
The effective capacitor between A and B in the following circuit is ______.

Explain the theory of an AC circuit with a resistor.
Where is the power dissipated in an alternating current circuit?
