Advertisements
Advertisements
प्रश्न
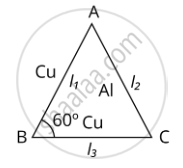
An equilateral triangle ABC is formed by two Cu rods AB and BC and one Al rod. It is heated in such a way that temperature of each rod increases by ∆T. Find change in the angle ABC. [Coeff. of linear expansion for Cu is α1, Coeff. of linear expansion for Al is α2]
उत्तर
We can solve this by using trigonometry
`cos theta = (1_1^2 + l_3^2 - l_2^2)/(2l_1l_3)`
`2l_1 1_3 = 1_1^2 + l_3^2 - l_2^2`
Now, differentiating both sides:
`2[d(1_1 1_3) xx cos theta + 1_1 1_3 d(cos theta)] = 2l_1dl_1 + 2l_3dl_3 - 2l_2dl_2`
`2[(1_1dl_3 + 1_3dl_1) cos theta - 1_1 1_3 sin theta d theta] = 2(1_1dl_1 + l_3dl_3 - 1_2dl_2)`
`(1_1dl_3 + 1_3dl_1) cos theta - 1_1 1_3 sin theta d theta = 1_1dl_1 + 1_3dl_3 - 1_2dl_2`
`L_t = L_0(1 + αΔt)`
`L_t = L_0 = L_0 αΔt`
`ΔL = Lα xx Δt`
`dl_1 = 1_1α_1 Δt, dl_3 = 1_2α_1Δt`
`dl_2 = 1_2α_2 Δt`
`1_1 = 1_2 = 1_3 = 1`
`dl_1 = 1l_1Δt, dl_3 = 1α_1 Δt`
`dl_2 = 1α_2 Δt` .....(i)
Now, substitute in (i)
`cos theta (1^2 xx α_1 Δt + 1^2α_1 Δt) - 1^2 sin theta d theta = l^2α_1 Δt + l^2 α_1 Δt - 1^2 α_1 Δt`
`2l^2α_1 Δt cos theta - l^2 [sin theta xx d theta]`
= `1^2 [α_1 + α_1 - α_2]Δt`
`1^2 [2α_1 Δ cos 60^circ - sin 60^circ d theta] = 1^2 [α_1 - α_2] Δt`
`2α_1 Δt xx 1/2 - 2α_1 Δt + α_2 Δt = sqrt(3)/2 d theta`
`sqrt(3)/2 d theta = [α_1 - 2α_1 + α_2] Δt`
`d theta = (2(α_2 - α_1)Δt)/sqrt(3)` .....[∵ Δt = ΔT]
`d theta = (2(α_2 - α_1)ΔT)/sqrt(3)`
APPEARS IN
संबंधित प्रश्न
The dimension ML−1T−2 can correspond to
A vertical metal cylinder of radius 2 cm and length 2 m is fixed at the lower end and a load of 100 kg is put on it. Find (a) the stress (b) the strain and (c) the compression of the cylinder. Young modulus of the metal = 2 × 1011 N m−2.
The elastic limit of steel is 8 × 108 N m−2 and its Young modulus 2 × 1011 N m−2. Find the maximum elongation of a half-metre steel wire that can be given without exceeding the elastic limit.
A steel wire and a copper wire of equal length and equal cross-sectional area are joined end to end and the combination is subjected to a tension. Find the ratio of the stresses developed in the two wires .
In figure the upper wire is made of steel and the lower of copper. The wires have equal cross section. Find the ratio of the longitudinal strains developed in the two wires.

The two wires shown in figure are made of the same material which has a breaking stress of 8 × 108 N m−2. The area of cross section of the upper wire is 0.006 cm2 and that of the lower wire is 0.003 cm2. The mass m1 = 10 kg, m2 = 20 kg and the hanger is light. Find the maximum load that can be put on the hanger without breaking a wire. Which wire will break first if the load is increased?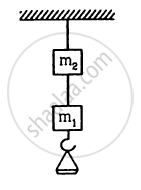
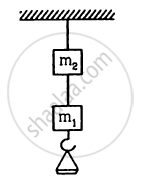
The two wires shown in figure are made of the same material which has a breaking stress of 8 × 108 N m−2. The area of cross section of the upper wire is 0.006 cm2 and that of the lower wire is 0.003 cm2. The mass m1 = 10 kg, m2 = 20 kg and the hanger is light. Repeat the above part if m1 = 10 kg and m2 = 36 kg.
Two persons pull a rope towards themselves. Each person exerts a force of 100 N on the rope. Find the Young modulus of the material of the rope if it extends in length by 1 cm. Original length of the rope = 2 m and the area of cross section = 2 cm2.
A steel wire of original length 1 m and cross-sectional area 4.00 mm2 is clamped at the two ends so that it lies horizontally and without tensions. If a load of 2.16 kg is suspended from the middle point of the wire, what would be its vertical depression ? Y of the steel = 2.0 × 1011 N m−2. Take g = 10 m s−2.
A wire of length L and radius r is clamped rigidly at one end. When the other end of the wire is pulled by a force f, its length increases by l. Another wire of the same material of length 2L and radius 2r, is pulled by a force 2f. Find the increase in length of this wire.
