Advertisements
Advertisements
प्रश्न
In nature, the failure of structural members usually result from large torque because of twisting or bending rather than due to tensile or compressive strains. This process of structural breakdown is called buckling and in cases of tall cylindrical structures like trees, the torque is caused by its own weight bending the structure. Thus the vertical through the centre of gravity does not fall within the base. The elastic torque caused because of this bending about the central axis of the tree is given by `(Ypir^4)/(4R) . Y` is the Young’s modulus, r is the radius of the trunk and R is the radius of curvature of the bent surface along the height of the tree containing the centre of gravity (the neutral surface). Estimate the critical height of a tree for a given radius of the trunk.
उत्तर
According to the problem, the elastic torque or the bending torque is given and we have to find the torque caused by the weight due to bending.
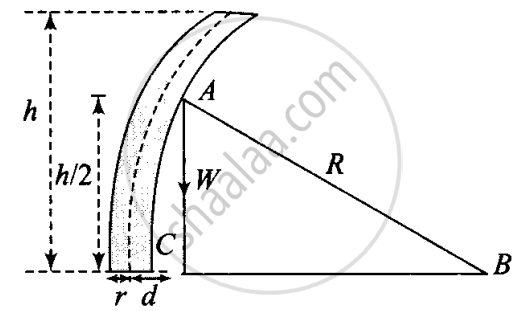
The diagram of the given situation is as shown.
The bending torque on the trunk of radius r of the tree = YπR4/4R where R is the radius of curvature of the bent surface.
`τ = Wd = (Ypir^4)/(4R)`
Here deforming torque is equal to elastic torque (restoring torque) caused by the bending of tree about its central axis when the tree is about to buckle.
Let h be the height of tree. If R >> h, then the centre of gravity of the tree is at a height of h/2 from the ground.
Refer to the figure in ΔABC
`R^2 = (R - d)^2 + (h/2)^2`
= `R^2 - 2Rd + d^2 + h^2/4`
Since, d << R, therefore the term d2 being very very small can be neglected.
∴ `R^2 = R^2 - 2Rd + h^2/d`
or `d = h^2/(8R)` ......(i)
If `omega_0` is the weight/volume, then
`(Ypir^4)/(4R) = omega_0 (pir^2h) h^2/(8R)` .....[∵ Torque is caused by the weight]
⇒ `h = ((2Y)/(omega_0))^(1/3) r^(2/3)`
Hence, critical height = `h = ((2Y)/(omega_0))^(1/3) r^(2/3)`.
APPEARS IN
संबंधित प्रश्न
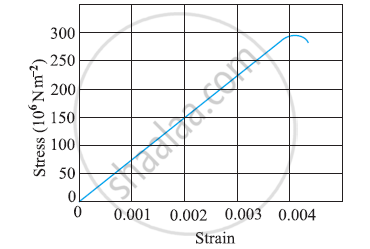
The figure shows the strain-stress curve for a given material. What are (a) Young’s modulus and (b) approximate yield strength for this material?
Read the following statements below carefully and state, with reasons, if it is true or false
The Young’s modulus of rubber is greater than that of steel;
Four identical hollow cylindrical columns of mild steel support a big structure of mass 50,000 kg. The inner and outer radii of each column are 30 cm and 60 cm respectively. Assuming the load distribution to be uniform, calculate the compressional strain of each column.
Two wires A and B are made of same material. The wire A has a length l and diameter rwhile the wire B has a length 2l and diameter r/2. If the two wires are stretched by the same force, the elongation in A divided by the elongation in B is
The length of a metal wire is l1 when the tension in it T1 and is l2 when the tension is T2. The natural length of the wire is
A steel rod of cross-sectional area 4 cm2 and 2 m shrinks by 0.1 cm as the temperature decreases in night. If the rod is clamped at both ends during the day hours, find the tension developed in it during night hours. Young modulus of steel = 1.9 × 1011 N m−2.
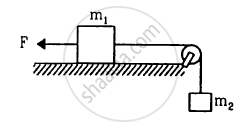
Consider the situation shown in figure. The force F is equal to the m2 g/2. If the area of cross section of the string is A and its Young modulus Y, find the strain developed in it. The string is light and there is no friction anywhere.
What is the Young’s modulus for a perfect rigid body ?
A steel rod (Y = 2.0 × 1011 Nm–2; and α = 10–50 C–1) of length 1 m and area of cross-section 1 cm2 is heated from 0°C to 200°C, without being allowed to extend or bend. What is the tension produced in the rod?
A steel rod of length 2l, cross sectional area A and mass M is set rotating in a horizontal plane about an axis passing through the centre. If Y is the Young’s modulus for steel, find the extension in the length of the rod. (Assume the rod is uniform.)
