Advertisements
Advertisements
प्रश्न
An isosceles triangle ABC has AC = BC. CD bisects AB at D and ∠CAB = 55°.
Find:
- ∠DCB
- ∠CBD
उत्तर
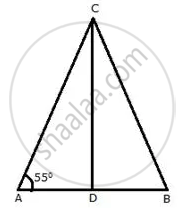
In ΔABC,
AC = BC ...[Given]
∴ ∠CAB = ∠CBD ...[angles opp. to equal sides are equal]
⇒ ∠CBD = 55°
In ΔABC,
∠CBA + ∠CAB + ∠ACB = 180°
but, ∠CAB = ∠CBA = 55°
⇒ 55° + 55° + ∠ACB = 180°
⇒ ∠ACB = 180° − 110°
⇒ ∠ACB = 70°
Now,
In ΔACD and ΔBCD,
AC = BC ...[Given]
CD = CD ...[Common]
AD = BD ...[Given: CD bisects AB]
∴ ΔACD ≅ ΔBCD
⇒ ∠DCA = ∠DCB
⇒ ∠DCB = `(∠"ACB")/2`
= `(70°)/2`
⇒ ∠DCB = 35°
APPEARS IN
संबंधित प्रश्न
In the figure given below, LM = LN; angle PLN = 110o.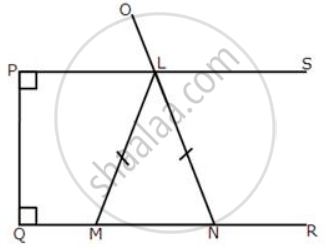
calculate: (i) ∠LMN
(ii) ∠MLN
Calculate x :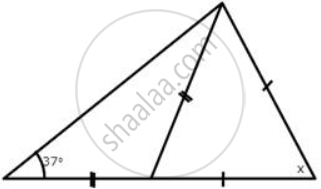
Calculate x :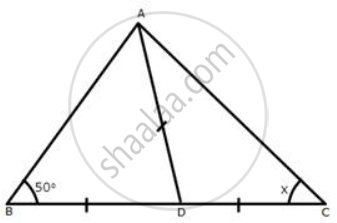
In the given figure; AB = BC and AD = EC.
Prove that: BD = BE.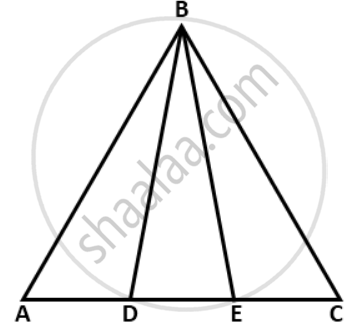
Prove that a triangle ABC is isosceles, if: altitude AD bisects angles BAC.
In triangle ABC; AB = AC and ∠A : ∠B = 8 : 5; find angle A.
Using the information given of the following figure, find the values of a and b.
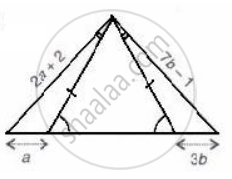
If the equal sides of an isosceles triangle are produced, prove that the exterior angles so formed are obtuse and equal.
Use the given figure to prove that, AB = AC.
The bisectors of the equal angles B and C of an isosceles triangle ABC meet at O. Prove that AO bisects angle A.
