Advertisements
Advertisements
प्रश्न
In triangle ABC; AB = AC and ∠A : ∠B = 8 : 5; find angle A.
उत्तर

Let ∠A = 8x and ∠B = 5x
Given: AB = AC
⇒ ∠B = ∠C = 5x ...[Angles opp. to equal sides are equal]
Now,
∠A + ∠B + ∠C = 180°
⇒ 8x + 5x + 5x = 180°
⇒ 18x = 180°
⇒ x = 10°
Given that :
∠A = 8x
⇒ ∠A = 8 x 10°
⇒ ∠A = 80°.
APPEARS IN
संबंधित प्रश्न
An isosceles triangle ABC has AC = BC. CD bisects AB at D and ∠CAB = 55°.
Find:
- ∠DCB
- ∠CBD
In the figure, given below, AB = AC.
Prove that: ∠BOC = ∠ACD.

Calculate x :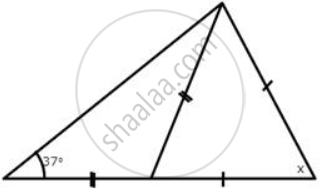
Calculate x :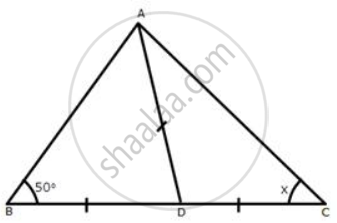
In the given figure; AB = BC and AD = EC.
Prove that: BD = BE.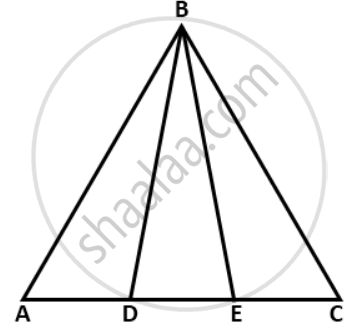
Prove that a triangle ABC is isosceles, if: bisector of angle BAC is perpendicular to base BC.
In the given figure, AD = AB = AC, BD is parallel to CA and angle ACB = 65°. Find angle DAC.
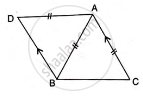
In isosceles triangle ABC, AB = AC. The side BA is produced to D such that BA = AD.
Prove that: ∠BCD = 90°
Prove that the medians corresponding to equal sides of an isosceles triangle are equal.
The bisectors of the equal angles B and C of an isosceles triangle ABC meet at O. Prove that AO bisects angle A.
