Advertisements
Advertisements
प्रश्न
भूमि के एक बिंदु से, जो मीनार के पाद-बिंदु से 30 मीटर की दूरी पर है, मीनार के शिखर का उन्नयन कोण 30° है। मीनार की ऊँचाई ज्ञात कीजिए।
उत्तर
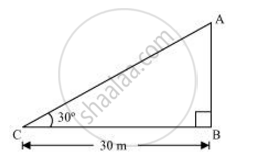
मान लीजिए कि AB मीनार है और बिंदु C (जमीन पर) से उन्नयन कोण 30° है।
ΔABC में,
`("AB")/("BC") = tan 30°`
`("AB")/30 = 1/sqrt3`
AB = `30/sqrt3`
AB = `30/sqrt3 xxsqrt3/sqrt3`
AB = `10sqrt3` m
इसलिए, मीनार की ऊँचाई `10sqrt3` मीटर है।
APPEARS IN
संबंधित प्रश्न
एक ठेकेदार बच्चों को खेलने के लिए एक पार्क में दो फिसलनपट्टी लगाना चाहती है। 5 वर्ष से कम उम्र के बच्चों के लिए वह एक ऐसी फिसलनपट्टी लगाना चाहती है जिसका शिखर 1.5m की ऊँचाई पर हो और भूमि के साथ 30° के कोण पर झुका हुआ हो, जबकि इससे अधिक उम्र के बच्चों के लिए वह 3m की ऊँचाई पर एक अधिक ढाल की फिसलनपट्टी लगाना चाहती है, जो भूमि के साथ 60° का कोण बनाती हो। प्रत्येक स्थिति में फिसलनपट्टी की लंबाई क्या होनी चाहिए?
1.5 म लंबा एक लड़का 30 म ऊँचे एक भवन से कुछ दूरी पर खड़ा है। जब वह ऊँचे भवन की ओर जाता है जब उसकी आँख से भवन के शिखर का उन्नयन कोण 30° से 60° हो जाता है। बताइए की वह भवन की ओर कितनी दूरी तक चलकर गया है।
7 m ऊँचे भवन के शिखर से एक केबल टॉवर के शिखर का उन्नयन कोण 60° है और इसके पाद का अवनमन कोण 45° है। टॉवर की ऊँचाई ज्ञात कीजिए।
एक 1.2 मीटर लंबी लड़की जमीन से 88.2 मीटर की ऊंचाई पर एक क्षैतिज रेखा में हवा के साथ चलते हुए एक गुब्बारे को देखती है। किसी भी क्षण लड़की की आँखों से गुब्बारे का उन्नयन कोण 60° होता है। कुछ समय बाद, उन्नयन कोण घटकर 30° हो जाता है। इस अंतराल के दौरान गुब्बारे द्वारा तय की गई दूरी ज्ञात कीजिए।

मीनार के आधार से और एक सरल रेखा में 4 m और 9 m की दूरी पर स्थित दो बिंदुओं से मीनार के शिखर के उन्नयन कोण पूरक कोण हैं। सिद्ध कीजिए की मीनार की ऊँचाई 6 m है।
6 m ऊँचे एक खंभे की छाया भूमि पर `2sqrt3` m लंबी है। तब, उस समय सूर्य का उन्नयन कोण ______ है।
यदि एक झील की सतह से 3 मीटर ऊपर एक प्लेटफार्म पर खड़ा एक व्यक्ति किसी बादल और झील में उसके परावर्तन को देखता है, तो उस बादल का उन्नयन कोण उसके परावर्तन के अवनमन कोण के बराबर होता है।
सूर्य का उस समय उन्नयन कोण ज्ञात कीजिए, जब h मीटर ऊँचे एक खंभे की छाया की लंबाई `sqrt(3)` h मीटर है।
किसी बिंदु से एक मीनार की चोटी का उन्नयन कोण 30° है। यदि प्रेक्षक दीवार की ओर 20 मीटर चलता है, तो उन्नयन कोण में 15° की वृद्धि हो जाती है। मीनार की ऊँचाई ज्ञात कीजिए।
एक ऊर्ध्वाधर मीनार एक क्षैतिज समतल पर खड़ी है तथा उस पर h ऊँचाई का एक ऊर्ध्वाधर ध्वज-दंड लगा हुआ है। समतल के किसी बिंदु से ध्वज-दंड के निचले और ऊपरी सिरों के उन्नयन कोण क्रमश : α और β हैं। सिद्ध कीजिए कि मीनार की ऊँचाई `((h tan alpha)/(tan beta - tan alpha))` है।
