Advertisements
Advertisements
प्रश्न
एक ठेकेदार बच्चों को खेलने के लिए एक पार्क में दो फिसलनपट्टी लगाना चाहती है। 5 वर्ष से कम उम्र के बच्चों के लिए वह एक ऐसी फिसलनपट्टी लगाना चाहती है जिसका शिखर 1.5m की ऊँचाई पर हो और भूमि के साथ 30° के कोण पर झुका हुआ हो, जबकि इससे अधिक उम्र के बच्चों के लिए वह 3m की ऊँचाई पर एक अधिक ढाल की फिसलनपट्टी लगाना चाहती है, जो भूमि के साथ 60° का कोण बनाती हो। प्रत्येक स्थिति में फिसलनपट्टी की लंबाई क्या होनी चाहिए?
उत्तर
यह देखा जा सकता है कि AC और PR क्रमशः छोटे और बड़े बच्चों के लिए फिसलनपट्टी हैं।
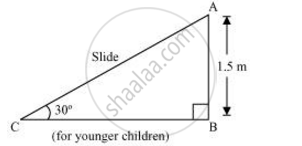
ΔABC में,
`("AB")/("AC")` = sin 30°
`1.5/("AC") = 1/2`
AC = 3 m
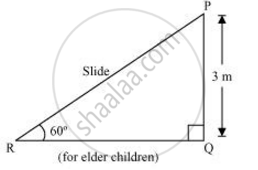
ΔPQR में,
`("PQ")/("PR")` = sin 60°
`3/("PR") = sqrt3/2`
PR = `6/sqrt3`
PR = `2sqrt3` m
इसलिए, इन फिसलनपट्टी की लंबाई 3 मीटर तथा `2sqrt3` m है।
APPEARS IN
संबंधित प्रश्न
एक मीनार के पाद-बिंदु से एक भवन के शिखर का उन्नयन कोण 30° है और भवन के पाद - बिंदु से मीनार के शिखर का उन्नयन कोण 60° है। यदि मीनार 50 m ऊँची हो, तो भवन को ऊंचाई ज्ञात कीजिए।
एक 80 m चौड़ी सड़क के दोनों ओर आमने-सामने समान लम्बाई वाले दो खंभे लगे हुए हैं। इन दोनों खंभों के बिच सड़क के एक बिंदु से खंभों के शिखर के उन्नयन कोण क्रमश: 60° और 30° हैं। खंभों की ऊँचाई और खंभों से बिंदु की दूरी ज्ञात कीजिए।
एक नहर के एक तट पर एक टीवी टॉवर ऊध्वार्रधरत: खड़ा है। टॉवर के ठीक सामने दूसरे तट के एक अन्य बिंदु से टॉवर के शिखर का उन्नयन कोण 60° है। इसी तट पर इस बिंदु से 20 m दूर और इस बिंदु को मीनार के पाद से मिलाने वाली रेखा पर स्थित एक अन्य बिंदु से टॉवर के शिखर का अन्नयन कोण 30° है। (आकृति देखिए) टॉवर की ऊँचाई और नहर की चौड़ाई ज्ञात कीजिए।

मीनार के आधार से और एक सरल रेखा में 4 m और 9 m की दूरी पर स्थित दो बिंदुओं से मीनार के शिखर के उन्नयन कोण पूरक कोण हैं। सिद्ध कीजिए की मीनार की ऊँचाई 6 m है।
15 मीटर लंबी एक सीढ़ी एक ऊर्ध्वाधर दीवार के ठीक ऊपरी सिरे पर पहुँच पाती है। यदि सीढ़ी इस समय दीवार से 60° का कोण बनाती है, तो दीवार की ऊँचाई ज्ञात कीजिए।
किसी मीनार के आधार से s और t की दूरियों पर स्थित दो बिंदुओं से मीनार की चोटी के उन्नयन कोण परस्पर पूरक हैं। सिद्ध कीजिए कि मीनार की ऊँचाई `sqrt(st)` है।
30 m ऊँची एक मीनार की चोटी का उसी समतल भूमि पर खड़ी मीनार के आधार से उन्नयन कोण 60° है तथा दूसरी मीनार की चोटी का पहली मीनार के आधार से उन्नयन कोण 30° है। दोनों मीनारों के बीच की दूरी ज्ञात कीजिए तथा दूसरी मीनार की ऊँचाई भी ज्ञात कीजिए।
h ऊँचाई की किसी मीनार की चोटी से दो वस्तुओं, जो मीनार के आधार वाली रेखा में स्थित हैं, के अवनमन कोण α और β (β > α) हैं। दोनों वस्तुओं के बीच की दूरी ज्ञात कीजिए।
किसी ऊर्ध्वाधर मीनार की चोटी का भूमि पर स्थित किसी बिंदु से उन्नयन कोण 60° है। पहले बिंदु से 10 m उर्ध्वाधरत: ऊपर एक अन्य बिंदु पर उसका उन्नयन कोण 45° है। मीनार की उँचाई ज्ञात कीजिए।
किसी मकान की निचली खिड़की भूमि से 2 m की ऊँचाई पर है तथा उसकी ऊपरी खिड़की निचली खिड़की से ऊर्ध्वाधरत : 4 m ऊपर है। किसी क्षण इन खिड़कियों से एक गुब्बारे के उन्नयन कोण क्रमश : 60° और 30° प्रेक्षित किए गए। भूमि के ऊपर गुब्बारे की ऊँचाई ज्ञात कीजिए।
