Advertisements
Advertisements
प्रश्न
किसी मकान की निचली खिड़की भूमि से 2 m की ऊँचाई पर है तथा उसकी ऊपरी खिड़की निचली खिड़की से ऊर्ध्वाधरत : 4 m ऊपर है। किसी क्षण इन खिड़कियों से एक गुब्बारे के उन्नयन कोण क्रमश : 60° और 30° प्रेक्षित किए गए। भूमि के ऊपर गुब्बारे की ऊँचाई ज्ञात कीजिए।
उत्तर
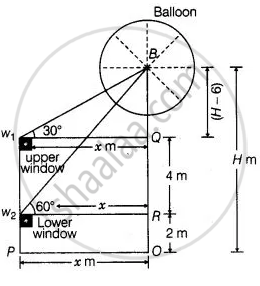
माना कि जमीन के ऊपर से गुब्बारे की ऊंचाई H है।
A और OP = w2R = w1Q = x
दिया गया है कि, जमीन के ऊपर से निचली खिड़की की ऊंचाई = w2P = 2 m = OR
निचली खिड़की के ऊपर से ऊपरी खिड़की की ऊंचाई = w1w2 = 4 m = QR
∴ BQ = OB – (QR + RO)
= H – (4 + 2)
= H – 6
और ∠Bw1Q = 30°
⇒ ∠Bw2R = 60°
अब, ΔBw2R में,
tan 60° = `"BR"/("w"_2"R") = ("BQ" + "QR")/x`
⇒ `sqrt(3) = (("H" - 6) + 4)/x`
⇒ `x = ("H" - 2)/sqrt(3)` ...(i)
और ΔBw1Q में,
tan 30° = `"BQ"/("w"_1"Q")`
tan 30° = `("H" - 6)/x = 1/sqrt(3)`
⇒ `x = sqrt(3)("H" - 6)` ...(ii)
समीकरण (i) और (ii) से,
`sqrt(3)("H" - 6) = (("H" - 2))/sqrt(3)`
⇒ 3(H – 6) = H – 2
⇒ 3H – 18 = H – 2
⇒ 2H = 16
⇒ H = 8
तो, आवश्यक ऊँचाई 8 m है।
अतः, जमीन के ऊपर से गुब्बारे की आवश्यक ऊंचाई 8 m है।
APPEARS IN
संबंधित प्रश्न
आँधी आने से एक पेड़ टूट जाता है और टूटा हुआ भाग इस तरह मुड़ जाता है की पेड़ का शिखर जमीन को छूने लगता है और इसके साथ 30° का कोण बनाता है। पेड़ के पाद-बिंदु की दूरी, जहाँ पेड़ का शिखर जमीन को छूता है, 8 मीटर है। पेड़ की उँचाई ज्ञात कीजिए।
भूमि से 60 m की ऊँचाई पर एक पतंग उड़ रही है। पतंग में लगी डोरी को अस्थायी रूप से भूमि के एक बिंदु से बांध से दिया गया है। भूमि के साथ डोरी का झुकाव 60° है। यह मानकर की डोरी में कोई ढील नहीं है, डोरी की लंबाई ज्ञात कीजिए।
1.5 म लंबा एक लड़का 30 म ऊँचे एक भवन से कुछ दूरी पर खड़ा है। जब वह ऊँचे भवन की ओर जाता है जब उसकी आँख से भवन के शिखर का उन्नयन कोण 30° से 60° हो जाता है। बताइए की वह भवन की ओर कितनी दूरी तक चलकर गया है।
एक नहर के एक तट पर एक टीवी टॉवर ऊध्वार्रधरत: खड़ा है। टॉवर के ठीक सामने दूसरे तट के एक अन्य बिंदु से टॉवर के शिखर का उन्नयन कोण 60° है। इसी तट पर इस बिंदु से 20 m दूर और इस बिंदु को मीनार के पाद से मिलाने वाली रेखा पर स्थित एक अन्य बिंदु से टॉवर के शिखर का अन्नयन कोण 30° है। (आकृति देखिए) टॉवर की ऊँचाई और नहर की चौड़ाई ज्ञात कीजिए।

7 m ऊँचे भवन के शिखर से एक केबल टॉवर के शिखर का उन्नयन कोण 60° है और इसके पाद का अवनमन कोण 45° है। टॉवर की ऊँचाई ज्ञात कीजिए।
मीनार के आधार से और एक सरल रेखा में 4 m और 9 m की दूरी पर स्थित दो बिंदुओं से मीनार के शिखर के उन्नयन कोण पूरक कोण हैं। सिद्ध कीजिए की मीनार की ऊँचाई 6 m है।
6 m ऊँचे एक खंभे की छाया भूमि पर `2sqrt3` m लंबी है। तब, उस समय सूर्य का उन्नयन कोण ______ है।
यदि एक झील की सतह से 3 मीटर ऊपर एक प्लेटफार्म पर खड़ा एक व्यक्ति किसी बादल और झील में उसके परावर्तन को देखता है, तो उस बादल का उन्नयन कोण उसके परावर्तन के अवनमन कोण के बराबर होता है।
यदि एक मीनार की ऊँचाई तथा उसके आधार से प्रेक्षण बिंदु की दूरी दोनों ही 10% बढ़ जाते हैं, तो चोटी का उन्नयन कोण वही रहता है।
h ऊँचाई की किसी मीनार की चोटी से दो वस्तुओं, जो मीनार के आधार वाली रेखा में स्थित हैं, के अवनमन कोण α और β (β > α) हैं। दोनों वस्तुओं के बीच की दूरी ज्ञात कीजिए।
