Advertisements
Advertisements
प्रश्न
किसी मीनार के आधार से s और t की दूरियों पर स्थित दो बिंदुओं से मीनार की चोटी के उन्नयन कोण परस्पर पूरक हैं। सिद्ध कीजिए कि मीनार की ऊँचाई `sqrt(st)` है।
उत्तर
माना मीनार की ऊँचाई h है।
और ∠ABC = θ
दिया गया है कि, BC = s, PC = t
और दोनों स्थितियों पर उन्नयन कोण पूरक हैं।
अर्थात्, ∠APC = 90° – θ ...[यदि दो कोण एक दूसरे के पूरक हैं, तो दोनों कोणों का योग 90° के बराबर होता है।]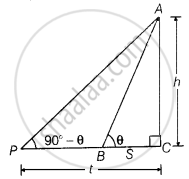
अब ΔABC में,
tan θ = `"AC"/"BC" = "h"/"s"` ...(i)
और ΔAPC में,
tan(90° – θ) = `"AC"/"PC"` ...[∵ tan(90° – θ) = cot θ]
⇒ cot θ = `"h"/"t"`
⇒ `1/tanθ = "h"/"t"` `[because cot θ = 1/(tan θ)]` ...(ii)
समीकरणों (i) और (ii) को गुणा करने पर, हमें प्राप्त होता है।
`tan θ * 1/tanθ = "h"/"s" * "h"/"t"`
⇒ `"h"^2/("st")` = 1
⇒ h2 = st
⇒ h = `sqrt("st")`
तो, मीनार की अभीष्ट ऊँचाई `sqrt("st")` है।
अत: सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
आँधी आने से एक पेड़ टूट जाता है और टूटा हुआ भाग इस तरह मुड़ जाता है की पेड़ का शिखर जमीन को छूने लगता है और इसके साथ 30° का कोण बनाता है। पेड़ के पाद-बिंदु की दूरी, जहाँ पेड़ का शिखर जमीन को छूता है, 8 मीटर है। पेड़ की उँचाई ज्ञात कीजिए।
एक पेडस्टल के शिखर पर एक 1.6 मीटर ऊँची मूर्ति लगी है। भूमि के एक बिंदु से मूर्ति के शिखर का उन्नयन कोण 60° है और उसी बिंदु से पेडस्टल के शिखर का उन्नयन कोण 45° है। पेडस्टल की ऊँचाई ज्ञात कीजिए।
एक मीनार के पाद-बिंदु से एक भवन के शिखर का उन्नयन कोण 30° है और भवन के पाद - बिंदु से मीनार के शिखर का उन्नयन कोण 60° है। यदि मीनार 50 m ऊँची हो, तो भवन को ऊंचाई ज्ञात कीजिए।
7 m ऊँचे भवन के शिखर से एक केबल टॉवर के शिखर का उन्नयन कोण 60° है और इसके पाद का अवनमन कोण 45° है। टॉवर की ऊँचाई ज्ञात कीजिए।
एक 1.2 मीटर लंबी लड़की जमीन से 88.2 मीटर की ऊंचाई पर एक क्षैतिज रेखा में हवा के साथ चलते हुए एक गुब्बारे को देखती है। किसी भी क्षण लड़की की आँखों से गुब्बारे का उन्नयन कोण 60° होता है। कुछ समय बाद, उन्नयन कोण घटकर 30° हो जाता है। इस अंतराल के दौरान गुब्बारे द्वारा तय की गई दूरी ज्ञात कीजिए।

यदि एक मीनार की छाया की लंबाई बढ़ रही है, तो सूर्य का उन्नयन कोण भी बढ़ रहा है।
यदि एक मीनार की ऊँचाई तथा उसके आधार से प्रेक्षण बिंदु की दूरी दोनों ही 10% बढ़ जाते हैं, तो चोटी का उन्नयन कोण वही रहता है।
सूर्य का उस समय उन्नयन कोण ज्ञात कीजिए, जब h मीटर ऊँचे एक खंभे की छाया की लंबाई `sqrt(3)` h मीटर है।
h ऊँचाई की किसी मीनार की चोटी से दो वस्तुओं, जो मीनार के आधार वाली रेखा में स्थित हैं, के अवनमन कोण α और β (β > α) हैं। दोनों वस्तुओं के बीच की दूरी ज्ञात कीजिए।
किसी ऊर्ध्वाधर मीनार की चोटी का भूमि पर स्थित किसी बिंदु से उन्नयन कोण 60° है। पहले बिंदु से 10 m उर्ध्वाधरत: ऊपर एक अन्य बिंदु पर उसका उन्नयन कोण 45° है। मीनार की उँचाई ज्ञात कीजिए।
