Advertisements
Advertisements
प्रश्न
बिंदुओं A(-2, 2) और B(2, 8) को जोड़ने वाले रेखाखंड AB को चार बराबर भागों में विभाजित करने वाले बिंदुओं के निर्देशांक ज्ञात कीजिए।
उत्तर १

बिंदु P, Q, R रेखाखंड को क्रमशः 1:3, 1:1, 3:1 के अनुपात में विभाजित किया गया हैं।
P के निर्देशांक = `((1xx2+3xx(-2))/(1+3),(1xx8+3xx2)/(1+3))`
`= (-1, 7/2)`
Q के निर्देशांक = `((2+(-2))/2, (2+8)/2)`
= (0,5)
R के निर्देशांक = `((3xx2+1xx(-2))/(3+1), (3xx8+1xx2)/(3+1))`
`=(1,13/2)`
उत्तर २
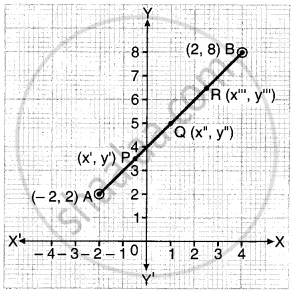
जैसा कि आकृति में दिखाया गया है। मान लीजिए A(-2, 2) और B(2, 8) को मिलाने वाले रेखाखंड को चार बराबर भागों में विभाजित करने वाले बिन्दु क्रमशः P(x’, y’), Q(x”, y”) एवं R(x”‘, y'”) हैं।
चूँकि यहाँ Q रेखाखंड AB का मध्य बिन्दु है।
⇒ x" = `(-2 + 2)/2 = 0/2 = 0`
एवं y" = `(2 + 8)/2 = 10/2 = 5`
Q के निर्देशांक (0, 5) हैं।
अब P रेखाखंड AQ का मध्य-बिन्दु है
⇒ x' = `(-2 + 0)/2 = (-2)/2 = -1`
एवं y' = `(2 + 5)/2 = 7/2`
एवं R रेखाखंड QB का मध्य-बिन्दु है
⇒ x"' = `(0 + 2)/2 = 2/2 = 1`
एवं y"' = `(5 + 8)/2 = 13/2`
अतः रेखाखंड AB को चार बराबर भागों में विभाजित करने वाले बिन्दु क्रमशः `(-1, 7/2)` (0, 5) एवं `(1, 13/2)` हैं।
APPEARS IN
संबंधित प्रश्न
यदि बिंदु P बिंदुओं A(-1, 7) और B(4,- 3) को जोड़ने वाले रेखाखंड को 2 : 3 अनुपात में विभाजित करता हो तो बिंदु P के निर्देशांक ज्ञात कीजिए।
नीचे दिए गए उदाहरण में रेखाखंड PQ को a : b के अनुपात में विभाजित करने वाले बिंदु A के निर्देशांक ज्ञात कीजिए।
P(-2, -5), Q(4, 3), a : b = 3 : 4
बिंदु A(8, 9) और B(1, 2) को जोड़ने वाले रेखाखंड AB को बिंदु P(k, 7) किस अनुपात में विभाजित करता है ज्ञात कीजिए और k का मान बताइए।
A(-14, -10), B(6, -2) को जोड़ने वाले रेखाखंड AB को चार सर्वांगसम रेखाखंडों में विभाजित करने वाले बिंदुओं के निर्देशांक ज्ञात कीजिए।
बिंदुओ (−2, 4, 7) और (3, –5, 8) को मिलाने वाली रेखा खंड, YZ-तल द्वारा जिस अनुपात में विभक्त होता है, उसे ज्ञात कीजिए।
विभाजन सूत्र का प्रयोग करके दिखाइए कि बिंदु
A(2, –3, 4), B(−1, 2, 1) तथा C`(0, 1/3, 2)` संरेख हैं।
P(4, 2, –6) और Q(10, –16, 6) के मिलाने वाली रेखा खंड PQ को सम त्रि-भाजित करने वाले बिंदुओं के निर्देशांक ज्ञात कीजिए।
यदि A और B क्रमशः (-2, -2) और (2, -4) हो तो बिंदु P के निर्देशांक ज्ञात कीजिए ताकि AP = `3/7` AB हो और P रेखाखंड AB पर स्थित हो।
यदि बिंदु (1, 2), (4, y), (x, 6) और (3, 5), इसी क्रम में लेने पर, एक समांतर चतुर्भुज के शीर्ष हो तो x और y ज्ञात कीजिए।
बिंदुओं A(2, -2) और B(3, 7) को जोड़ने वाले रेखाखंड को रेखा 2x + y - 4 = 0 जिस अनुपात में विभाजित करती है उसे ज्ञात कीजिए।
