Advertisements
Advertisements
प्रश्न
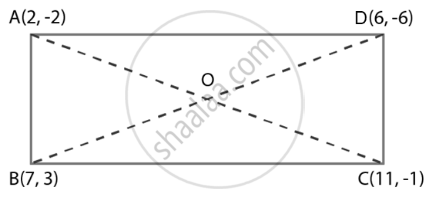
बिंदुओं A(2, –2), B(7, 3), C(11, –1) और D(6, –6) को इसी क्रम में लेने पर किस प्रकार का चतुर्भुज बनता है?
Advertisements
उत्तर
बिंदु A(2, –2), B(7, 3), C(11, –1) और D(6, –6) हैं।
दूरी सूत्र का प्रयोग करके,
d = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`
AB = `sqrt((7 - 2)^2 + (3 + 2)^2`
= `sqrt((5)^2 + (5)^2`
= `sqrt(25 + 25)`
= `sqrt(50)`
= 5`sqrt(2)`
BC = `sqrt((11 - 7)^2 + (-1 - 3)^2`
= `sqrt((4)^2 + (-4)^2`
= `sqrt(16 + 16)`
= `sqrt(32)`
= `4sqrt(2)`
CD = `sqrt((6 - 11)^2 + (-6 + 1)^2`
= `sqrt((-5)^2 + (-5)^2`
= `sqrt(25 + 25)`
= `sqrt(50)`
= `5sqrt(2)`
DA = `sqrt((2 - 6)^2 + (-2 + 6)^2`
= `sqrt((-4)^2 + (4)^2`
= `sqrt(16 + 16)`
= `sqrt(32)`
= `4sqrt(2)`
विकर्ण AC तथा BD ज्ञात करने पर, हमें प्राप्त होता है,
AC = `sqrt((11 - 2)^2 + (-1 + 2)^2`
= `sqrt((9)^2 + (1)^2`
= `sqrt(81 + 1)`
= `sqrt(82)`
और BD = `sqrt((6 - 7)^2 + (-6 - 3)^2`
= `sqrt((-1)^2 + (-9)^2`
= `sqrt(1 + 81)`
= `sqrt(82)`
APPEARS IN
संबंधित प्रश्न
किसी त्रिभुज के शीर्षबिंदु A(-3,1), B(0,-2) और C(1,3) हों तो इस त्रिभुज के परिकेंद्र के निर्देशांक ज्ञात कीजिए।
सिद्ध कीजिए कि, बिंदु P(1, −2), Q(5, 2), R(3, −1) और S(−1, −5) समांतर चतुर्भुज के शीर्षबिंदु हैं।
निम्नलिखित बिंदुओं द्वारा बनने वाले चतुर्भुज का प्रकार (यदि कोई है तो) बताइए तथा अपने उत्तर के लिए कारण भी दीजिए:
(-3, 5), (3, 1), (0, 3), (-1, -4)
x-अक्ष पर वह बिंदु ज्ञात कीजिए जो (2, -5) और (-2, 9) से समदूरस्थ हैं।
किसी वर्ग के दो सम्मुख शीर्ष (-1, 2) और (3, 2) हैं। वर्ग के अन्य दोनों शीर्ष ज्ञात कीजिए।
बिंदुओं A(0, 6) और B(0, –2) के बीच की दूरी ______ है।
AOBC एक आयत है, जिसके तीन शीर्ष A(0, 3), O(0, 0) और B(5, 0) हैं। इसका विकर्ण ______ हैं।
बिंदुओं A(–2, –5) और B(2, 5) को मिलाने वाले रेखाखंड के लंब समद्विभाजक पर स्थित एक बिंदु ______ है।
एक वृत्त का केंद्र मूलबिंदु पर है तथा एक बिंदु P(5, 0) इस वृत्त पर स्थित है। बिंदु Q(6, 8) इस वृत्त के बाहर स्थित है।
बिंदु A(2, 7), बिंदुओं P(6, 5) और Q(0, – 4) को मिलाने वाले रेखाखंड के लंब समद्विभाजक पर स्थित है।
